2.4 Complex numbers: representing complex numbers in a vector space

So far we have coded the complex number $z=x+jy$ with the Cartesianpair $(x,y)$ and with the polar pair $\left(r\angle \theta \right)$ . We now show how the complexnumber $z$ may be coded with a two-dimensional vector $z$ and show how this new code may be used to gain insight about complex numbers.

Coding a Complex Number as a Vector. We code the complex number $z=x+jy$ with the two-dimensional vector $z=xy$ :

We plot this vector as in [link] . We say that the vector $z$ belongs to a “vector space.” This means that vectors may be added and scaled according to the rules

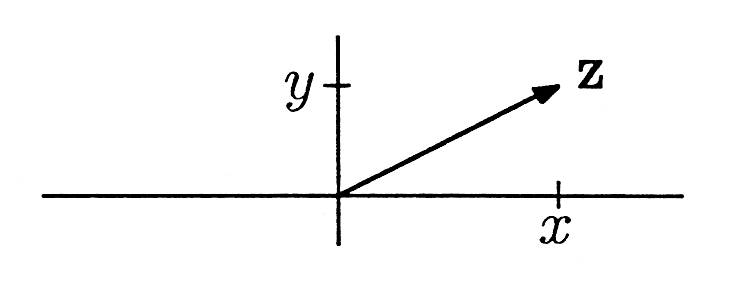
Furthermore, it means that an additive inverse $-z$ , an additive identity $0$ , and a multiplicative identity 1 all exist:

The vector $0$ is $0=00$ .

Prove that vector addition and scalar multiplication satisfy these properties of commutation, association, and distribution:

Inner Product and Norm. The inner product between two vectors $z_1$ and $z_2$ is defined to be the real number

We sometimes write this inner product as the vector product (more on this in Linear Algebra )

When $z_1=z_2=z$ , then the inner product between $z$ and itself is the norm squared of $z$ :

These properties of vectors seem abstract. However, as we now show, they may be used to develop a vector calculus for doing complex arithmetic.

A Vector Calculus for Complex Arithmetic. The addition of two complex numbers $z_1$ and $z_2$ corresponds to the addition of the vectors $z_1$ and $z_2$ :

The scalar multiplication of the complex number $z_2$ by the real number $x_1$ corresponds to scalar multiplication of the vector $z_2$ by $x_1$ :

Similarly, the multiplication of the complex number $z_2$ by the real number $y_1$ is

The complex product $z_1{z}_2=(x_1+j{y}_1)z_2$ is therefore represented as

This representation may be written as the inner product

where $v$ and $w$ are the vectors $v=x_2-y_2$ and $w=y_2{x}_2$ . By defining the matrix

we can represent the complex product $z_1{z}_2$ as a matrix-vector multiply (more on this in Linear Algebra ):

With this representation, we can represent rotation as

We call the matrix $cos\theta -sin\theta sin\theta cos\theta$ a “rotation matrix.”

Inner Product and Polar Representation. From the norm of a vector, we derive a formula for the magnitude of $z$ in the polar representation $z=r{e}^{j\theta }$ :

If we define the coordinate vectors $e_1=10$ and $e_2=01$ , then we can represent the vector $z$ as

See [link] . From the figure it is clear that the cosine and sine of the angle $\theta$ are

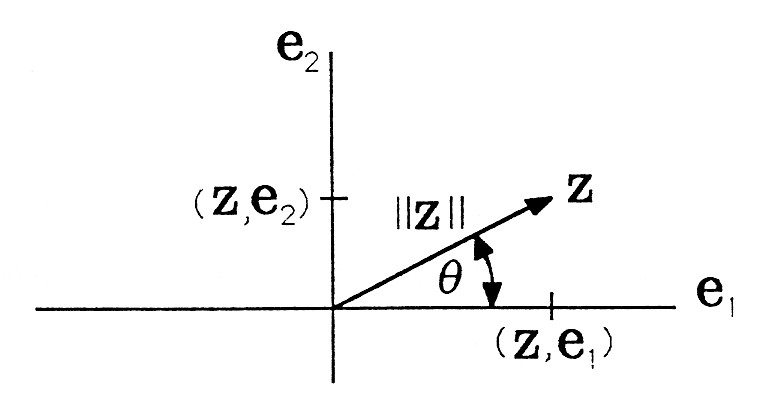
This gives us another representation for any vector $z$ :

The inner product between two vectors $z_1$ and $z_2$ is now

It follows that $cos({\theta }_2-{\theta }_1)=cos{\theta }_2$ cos ${\theta }_1+sin{\theta }_{1}sin{\theta }_2$ may be written as

This formula shows that the cosine of the angle between two vectors $z_1$ and $z_2$ , which is, of course, the cosine of the angle of $z_2{z}_1^{*}$ , is the ratio of the inner product to the norms.