| << Chapter < Page | Chapter >> Page > |
Sinusoidal signals are perhaps the most important type of signal that we will encounter in signal processing. There are two basic types of signals, the cosine :
and the sine :
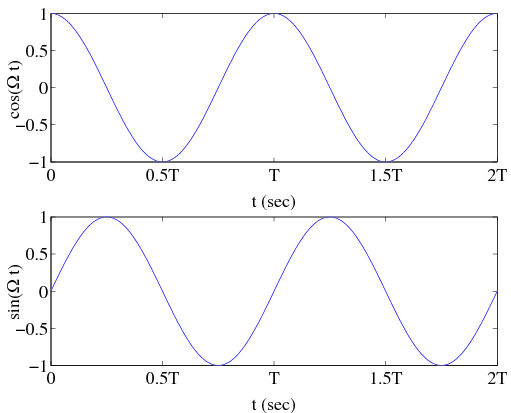
where is a real constant. Plots of the sine and cosine signals are shown in [link] . Sinusoidal signals are periodic signals. The period of the cosine and sine signals shown above is given by . The frequency of the signals is which has units of rad/sec . Equivalently, the frequency can be expressed as , which has units of , cycles/sec , or Hz . The quantity has units of radians and is often called the phase of the sinusoid. Recalling the effect of a time shift on the appearance of a signal, we can observe from [link] that the sine signal is obtained by shifting the cosine signal by seconds, i.e.
and since , we have
Similarly, we have
Using Euler's Identity, we can also write:
and
The quantity is called a complex sinusoid and can be expressed as
There are a number of trigonometric identities which are sometimes useful. These are shown in [link] . [link] shows some basic calculus operations on sine and cosine signals.
Now suppose that we have a sum of two sinusoids, say
It is of interest to know what the period of the sum of 2 sinusoids is. We must have
It follows that and , where and are integers. Solving these two equations for gives . We wish to select the shortest possible period, since any integer multiple of the period is also a period. To do this we note that since , we can write
so we seek the smallest integers and that satisfy [link] . This can be done by finding the greatest common divisor between and . For example if and , we have and , after dividing out 5, the greatest common divisor between 10 and 15. So the period is sec. On the other hand, if and , we find that and and the period increases to sec. Notice also that if the ratio of and is not a rational number, then is not periodic!
If there are more than two sinusoids, it is probably easiest to find the period of one pair of sinusoids at a time, using the two lowest frequencies (which will have a longer period). Once the frequency of the first two sinusoids has been found, replace them with a single sinusoid at the composite frequency corresponding to the first two sinusoids and compare it with the third sinusoid, and so on.

Notification Switch
Would you like to follow the 'Signals, systems, and society' conversation and receive update notifications?