| << Chapter < Page | Chapter >> Page > |

analysis for to get a wavelet basis for . [link] does not hold with replaced by because is bigger than the direct sum of the constituents at the next coarser scale. Let be this difference space:
If we can find an orthonormal basis for , then we have a multiresolution analysis for .
We proceed as follows. Construct entry filters (for the analysis filters) of the filter bank with synthesis filters . Time-reverse them to obtain entry filters (for the synthesis filters).If is the McMillan degree of the synthesis bank, there are entry filters. Let denote the synthesis entry filters. Define the entry functions
is compactly supported in . Let . By considering one stage of the analysis and synthesis stages of this PR filter bank on right sided signals),it readily follows that [link] holds. Therefore
forms a wavelet tight frame for . If one started with an ON basis for , the newly constructed basis is an ON basis for . Indeed if is an orthonormal system
and
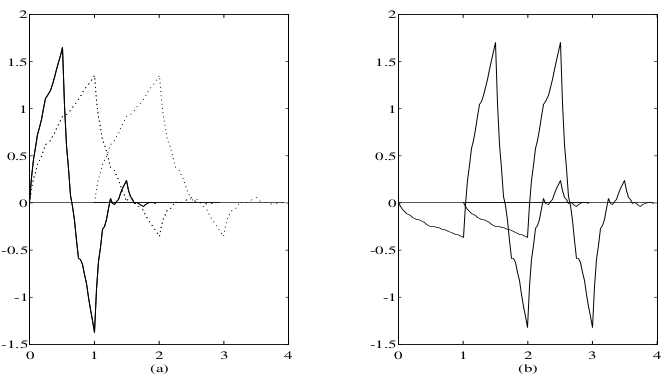
The dimension of is precisely the McMillan degree of the polyphase component matrix of the scaling and wavelet filters considered as the filters of the synthesis bank . There are precisely as many entry functions as there are entry filters,and supports of these functions are explicitly given in terms of the lengths of the corresponding entry filters. [link] shows the scaling function, wavelet, their integer translates and the single entry function corresponding to Daubechies four coefficient wavelets. In this case, .
One could start with a wavelet basis for and reflect all the functions about . This is equivalent to swapping the analysis and synthesis filters of the filter bank. We give an independentdevelopment. We start with a WTF for with functions
supported in . Scaling and wavelet filters constitute the analysis bank in this case. Let be the McMillan degree of the analysis bank and let be the (analysis) exit filters. Define the exit functions
, and for . Then as , and
forms a WTF for . Orthonormality of this basis is equivalent to the orthonormality of its parent basis on the line.An example with one exit function (corresponding to , ) Type 1 modulated WTF obtained earlier is given in [link] .
Using the ideas above, one can construct wavelet bases for the interval and consequently segmented wavelet bases for . One can write as a disjoint union of intervals and use a different wavelet basis in each interval. Each interval is will be spanned bya combination of scaling functions, wavelets, and corresponding entry and exit functions. For instance [link] and [link] together correspond to a wavelet basis for , where a 3-band wavelet basis with length-6 filters is used for and a 2-band wavelet basis with length-4 filters is used for . Certainly a degree of overlap between the exit functions on the left of a transition and entryfunctions on the right of the transition can be obtained by merely changing coordinates in the finite dimensional space corresponding to these functions.Extension of these ideas to obtain segmented wavelet packet bases is also immediate.

Notification Switch
Would you like to follow the 'Wavelets and wavelet transforms' conversation and receive update notifications?