0.1 Digital filter design

When designing digital filters for signal processing applications one is often interested in creating objects $h\in {\mathbb{R}}^N$ in order to alter some of the properties of a given vector $x\in {\mathbb{R}}^M$ (where $0<M,N<\infty$ ). Often the properties of $x$ that we are interested in changing lie in the frequency domain, with $X=\mathcal{F}\left(x\right)$ being the frequency domain representation of $x$ given by

where $A_X$ and ${\phi }_X$ are the amplitude and phase components of $x$ , and $\mathcal{F}(·):{\mathbb{R}}^N\mapsto {\mathbb{R}}^{\infty }$ is the Fourier transform operator defined by

So the idea in filter design is to create filters $h$ such that the Fourier transform $H$ of $h$ posesses desirable amplitude and phase characteristics.

The filtering operator is the convolution operator ( $*$ ) defined by

An important property of the convolution operator is the Convolution Theorem [link] which states that

where $\left\{A_X,,,{\phi }_X\right\}$ and $\left\{A_H,,,{\phi }_H\right\}$ represent the amplitude and phase components of $X$ and $H$ respectively. It can be seen that by filtering $x$ with $h$ one can apply a scaling operator to the amplitude of $x$ and a biasing operator to its phase.

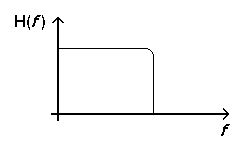
A common use of digital filters is to remove a certain band of frequencies from the frequency spectra of $x$ . Consider the lowpass filter from [link] ; note that only the desired amplitude response is shown (not the phase response). Other types of filters include band-pass , high-pass or band-reject filters, depending on the range of frequencies that they alter.

The notion of approximation in $l_p$ Filter design

Once a filter design concept has been selected (such as that from [link] ), the design problem becomes finding the optimal vector $h\in {\mathbb{R}}^n$ that most closely approximates our desired frequency response concept (we will denote such optimal vector by $h^{☆}$ ). This approximation problem will heavily depend on the measure by which we evaluate all vectors $h\in {\mathbb{R}}^N$ to choose $h^{☆}$ .

In this document we consider the discrete $l_p$ norms defined by

as measures of optimality, and consider a number of filter design problems based upon this criterion. The work explores the Iterative Reweighted Least Squares (IRLS) approach as a design tool, and provides a number of algorithms based on this method. Finally, this work considers critical theoretical aspects and evaluates the numerical properties of the proposed algorithms in comparison to existing general purpose methods commonly used. It is the belief of the author (as well as the author's advisor) that the IRLS approach offers a more tailored route to the $l_p$ filter design problems considered, and that it contributes an example of a made-for-purpose algorithm best suited to the characteristics of $l_p$ filter design.