2.1 Vectors in the plane (Page 6/29)

Calculus volume 3 Page 6 / 29

□

Prove the additive inverse property.

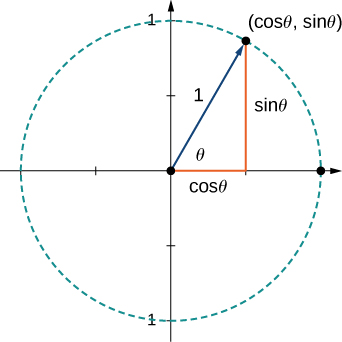
We have found the components of a vector given its initial and terminal points. In some cases, we may only have the magnitude and direction of a vector, not the points. For these vectors, we can identify the horizontal and vertical components using trigonometry ( [link] ).

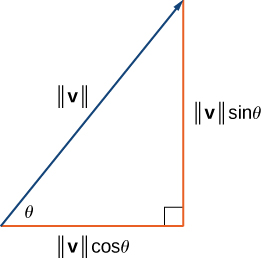
This figure is a right triangle. There is an angle labeled theta. The two sides are labeled “magnitude of v times cosine theta” and “magnitude of v times sine theta.” The hypotenuse is labeled “magnitude of v.” — The components of a vector form the legs of a right triangle, with the vector as the hypotenuse.

Consider the angle $θ$ formed by the vector v and the positive x -axis. We can see from the triangle that the components of vector $v$ are $⟨ ‖ v ‖ cos θ, ‖ v ‖ sin θ ⟩ .$ Therefore, given an angle and the magnitude of a vector, we can use the cosine and sine of the angle to find the components of the vector.

Finding the component form of a vector using trigonometry

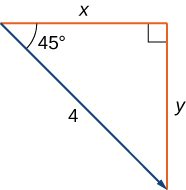
Find the component form of a vector with magnitude 4 that forms an angle of $−45 °$ with the x -axis.

Let $x$ and $y$ represent the components of the vector ( [link] ). Then $x = 4 cos (−45 °) = 2 \sqrt{2}$ and $y = 4 sin (−45 °) = −2 \sqrt{2} .$ The component form of the vector is $⟨ 2 \sqrt{2}, −2 \sqrt{2} ⟩ .$

This figure is a right triangle. The two sides are labeled “x” and “y.” The hypotenuse is labeled “4.” There is also an angle labeled “45 degrees.” The hypotenuse is represented as a vector. — Use trigonometric ratios, $x = ‖ v ‖ cos θ$ and $y = ‖ v ‖ sin θ,$ to identify the components of the vector.

Got questions? Get instant answers now!

Find the component form of vector $v$ with magnitude $10$ that forms an angle of $120 °$ with the positive x -axis.

$v = ⟨ −5, 5 \sqrt{3} ⟩$

Got questions? Get instant answers now!

Unit vectors

A unit vector is a vector with magnitude $1 .$ For any nonzero vector $v,$ we can use scalar multiplication to find a unit vector $u$ that has the same direction as $v .$ To do this, we multiply the vector by the reciprocal of its magnitude:

u = \frac{1}{‖ v ‖} v .

Recall that when we defined scalar multiplication, we noted that $‖ k v ‖ = | k | \cdot ‖ v ‖ .$ For $u = \frac{1}{‖ v ‖} v,$ it follows that $‖ u ‖ = \frac{1}{‖ v ‖} (‖ v ‖) = 1 .$ We say that $u$ is the unit vector in the direction of $v$ ( [link] ). The process of using scalar multiplication to find a unit vector with a given direction is called normalization .

This image has two figures. The first is a vector labeled “v.” The second figure is a vector in the same direction labeled “u.” This vector has a length of 1 unit. — The vector $v$ and associated unit vector $u = \frac{1}{‖ v ‖} v .$ In this case, $‖ v ‖ > 1 .$

Finding a unit vector

Let $v = ⟨ 1, 2 ⟩ .$

Find a unit vector with the same direction as $v .$
Find a vector $w$ with the same direction as $v$ such that $‖ w ‖ = 7 .$

First, find the magnitude of $v,$ then divide the components of $v$ by the magnitude:

$‖ v ‖ = \sqrt{1^{2} + 2^{2}} = \sqrt{1 + 4} = \sqrt{5}$

$u = \frac{1}{‖ v ‖} v = \frac{1}{\sqrt{5}} ⟨ 1, 2 ⟩ = ⟨ \frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}} ⟩ .$
The vector $u$ is in the same direction as $v$ and $‖ u ‖ = 1 .$ Use scalar multiplication to increase the length of $u$ without changing direction:

$w = 7 u = 7 ⟨ \frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}} ⟩ = ⟨ \frac{7}{\sqrt{5}}, \frac{14}{\sqrt{5}} ⟩ .$

Got questions? Get instant answers now!

Let $v = ⟨ 9, 2 ⟩ .$ Find a vector with magnitude $5$ in the opposite direction as $v .$

$⟨ - \frac{45}{\sqrt{85}}, - \frac{10}{\sqrt{85}} ⟩$

Got questions? Get instant answers now!

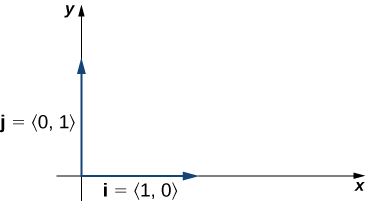
We have seen how convenient it can be to write a vector in component form. Sometimes, though, it is more convenient to write a vector as a sum of a horizontal vector and a vertical vector. To make this easier, let’s look at standard unit vectors. The standard unit vectors are the vectors $i = ⟨ 1, 0 ⟩$ and $j = ⟨ 0, 1 ⟩$ ( [link] ).

This figure has the x and y axes of a coordinate system in the first quadrant. On the x-axis there is a vector labeled “i,” which equals <1,0>. The second vector is on the y-axis and is labeled “j” which equals <0,1>. — The standard unit vectors $i$ and $j .$

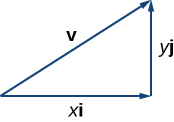
By applying the properties of vectors, it is possible to express any vector in terms of $i$ and $j$ in what we call a linear combination :

v = ⟨ x, y ⟩ = ⟨ x, 0 ⟩ + ⟨ 0, y ⟩ = x ⟨ 1, 0 ⟩ + y ⟨ 0, 1 ⟩ = x i + y j .

Thus, $v$ is the sum of a horizontal vector with magnitude $x,$ and a vertical vector with magnitude $y,$ as in the following figure.

This figure is a right triangle. The horizontal side is labeled “xi.” The vertical side is labeled “yj.” The hypotenuse is a vector labeled “v.” — The vector $v$ is the sum of $x i$ and $y j .$

Using standard unit vectors

Express the vector $w = ⟨ 3, −4 ⟩$ in terms of standard unit vectors.
Vector $u$ is a unit vector that forms an angle of $60 °$ with the positive x -axis. Use standard unit vectors to describe $u .$

Resolve vector $w$ into a vector with a zero y -component and a vector with a zero x -component:

$w = ⟨ 3, −4 ⟩ = 3 i - 4 j .$
Because $u$ is a unit vector, the terminal point lies on the unit circle when the vector is placed in standard position ( [link] ).

$\begin{matrix} u & = ⟨ cos 60 °, sin 60 ° ⟩ \\ = ⟨ \frac{1}{2}, \frac{\sqrt{3}}{2} ⟩ \\ = \frac{1}{2} i + \frac{\sqrt{3}}{2} j . \end{matrix}$

The terminal point of $u$ lies on the unit circle $(cos θ, sin θ) .$

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 19

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?

Ask

	Anthropology Life Cycle By Richley Crapo Start Assignment
	7 Sociology 07 Deviance, Crime, Social Control MCQ By OpenStax Start Quiz
	18 AP 18 Cardiovascular System Blood MCQ By OpenStax Start Quiz
	Social Dances 1 By Marion Cabalfin Start Test
	Art History ARTH209 20th Century By Rebecca Butterfield Start Quiz
	2 Pharmacology Nervous System Essay By Rohini Ajay Start Test
	Young Economist MCQ Test By Robert Murphy Start Test
	NCE Ch 10 Professional Orientation By Anh Dao Start Quiz
	14 AP 14 Brain Cranial Nerves Essay By OpenStax Start Flashcards
	How much do you love him? By Zarina Chocolate Start Quiz