| << Chapter < Page | Chapter >> Page > |
Research one of the following geometrical ideas and describe it to your group:
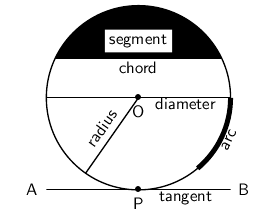
The following is a recap of terms that are regularly used when referring to circles.
An axiom is an established or accepted principle. For this section, the following are accepted as axioms.
A theorem is a general proposition that is not self-evident but is proved by reasoning (these proofs need not be learned for examination purposes).
Theorem 1 The line drawn from the centre of a circle, perpendicular to a chord, bisects the chord.
Proof :
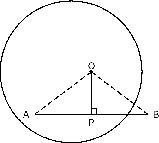
Consider a circle, with centre . Draw a chord and draw a perpendicular line from the centre of the circle to intersect the chord at point . The aim is to prove that =
Apply the Theorem of Pythagoras to each triangle, to get:
However, . So,
This means that bisects .
Theorem 2 The line drawn from the centre of a circle, that bisects a chord, is perpendicular to the chord.
Proof :
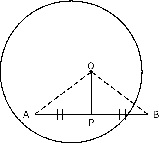
Consider a circle, with centre . Draw a chord and draw a line from the centre of the circle to bisect the chord at point . The aim is to prove that In and ,
(SSS).
Theorem 3 The perpendicular bisector of a chord passes through the centre of the circle.
Proof :
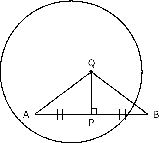
Consider a circle. Draw a chord . Draw a line perpendicular to such that bisects at point . Draw lines and . The aim is to prove that is the centre of the circle, by showing that . In and ,
(SAS). From this, . Since the centre of a circle is the only point inside a circle that has points on the circumference at an equal distance from it, must be the centre of the circle.

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 12 maths' conversation and receive update notifications?