| << Chapter < Page | Chapter >> Page > |
The Winograd Fourier transform algorithm (WFTA) uses a very powerful property of the Type-1 index map and the DFT to give afurther reduction of the number of multiplications in the PFA. Using an operator notation where represents taking row DFT's and represents column DFT's, the two-factor PFA of [link] is represented by
It has been shown [link] , [link] that if each operator represents identical operations on each row or column,they commute. Since and represent length and DFT's, they commute and [link] can also be written
If each short DFT in is expressed by three operators as in Winograd’s Short DFT Algorithms: Equation 8 and Winograd’s Short DFT Algorithms: Figure 2 , can be factored as
where A represents the set of additions done on each row or column that performs the residue reduction as Winograd’s Short DFT Algorithms: Equation 30 . Because of the appearance of the flow graph of and because it is the first operator on , it is called a preweave operator [link] . is the set of multiplications and (or or ) from Winograd’s Short DFT Algorithms: Equation 5 or Winograd’s Short DFT Algorithms: Equation 6 is the reconstruction operator called the postweave. Applying [link] to [link] gives
This is the PFA of [link] and [link] where represents the row DFT's on the array formed from . Because these operators commute, [link] can also be written as
or
but the two adjacent multiplication operators can be premultiplied and the result represented by oneoperator which is no longer the same for each row or column. Equation [link] becomes
This is the basic idea of the Winograd Fourier transform algorithm. The commuting of the multiplication operators together in the centerof the algorithm is called nesting and it results in a significant decrease in the number of multiplications that must be done at theexecution of the algorithm. Pictorially, the PFA of [link] becomes [link] the WFTA in [link] .
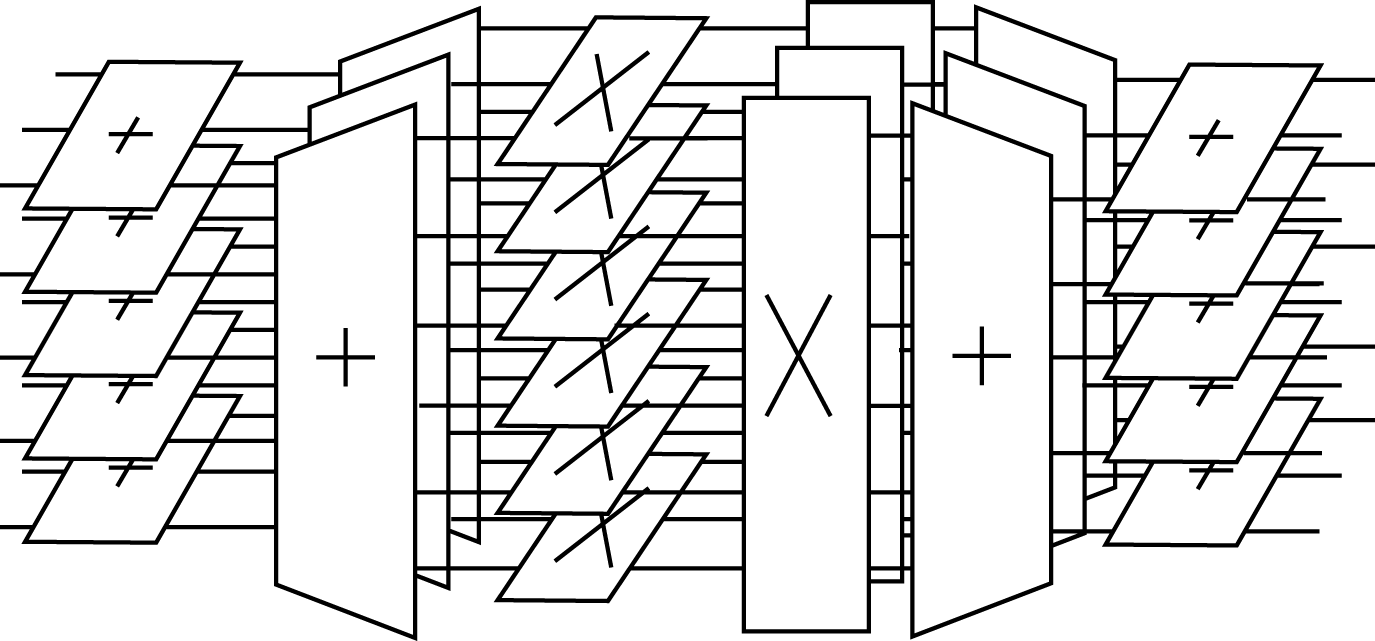
The rectangular structure of the preweave addition operators causes an expansion of the data in the center of the algorithm. The15 data points in [link] become 18 intermediate values. This expansion is a major problem in programming the WFTA because itprevents a straightforward in-place calculation and causes an increase in the number of required additions and in the number ofmultiplier constants that must be precalculated and stored.
From [link] and the idea of premultiplying the individual multiplication operators, it can be seen why the multiplications byunity had to be considered in Winograd’s Short DFT Algorithms: Table 1 . Even if a multiplier in is unity, it may not be in . In [link] with factors of three and five, there appear to be 18 multiplications requiredbecause of the expansion of the length-5 preweave operator, , however, one of multipliers in each of the length three and fiveoperators is unity, so one of the 18 multipliers in the product is unity. This gives 17 required multiplications - a rather impressivereduction from the multiplications required by direct calculation. This number of 17 complex multiplications will requireonly 34 real multiplications because, as mentioned earlier, the multiplier constants are purely real or imaginary while the 225complex multiplications are general and therefore will require four times as many real multiplications.

Notification Switch
Would you like to follow the 'Fast fourier transforms' conversation and receive update notifications?