| << Chapter < Page | Chapter >> Page > |
Recently several papers [link] , [link] , [link] , [link] , [link] have been published on algorithms to calculate a length- DFT more efficiently than a Cooley-Tukey FFT of any radix. They all havethe same computational complexity and are optimal for lengths up through 16 and until recently was thought to give the best total add-multiply countpossible for any power-of-two length. Yavne published an algorithm with the same computational complexity in 1968 [link] , but it went largely unnoticed. Johnson and Frigo have recently reported the firstimprovement in almost 40 years [link] . The reduction in total operations is only a few percent, but it is a reduction.
The basic idea behind the split-radix FFT (SRFFT) as derived by Duhamel and Hollmann [link] , [link] is the application of a radix-2 index map to the even-indexed terms and a radix-4 map to theodd- indexed terms. The basic definition of the DFT
with gives
for the even index terms, and
and
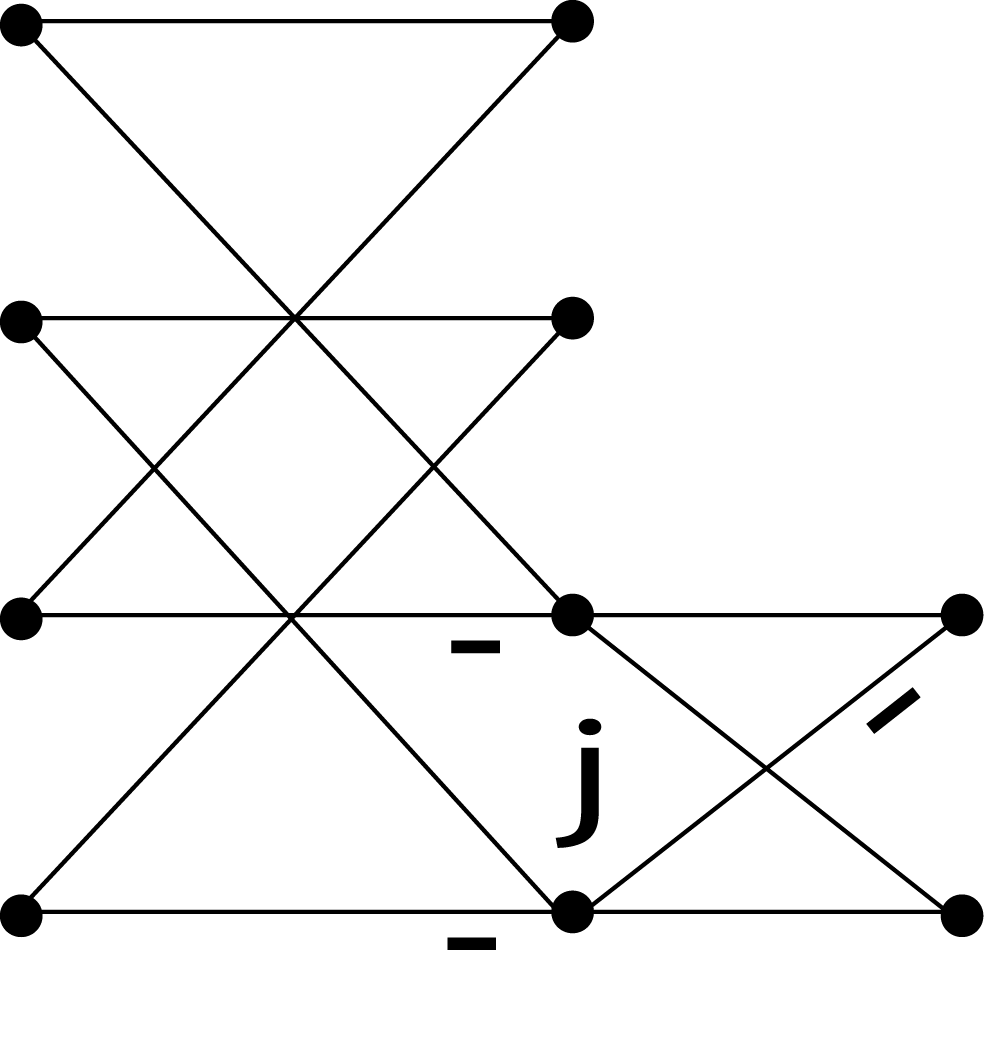
for the odd index terms. This results in an L-shaped “butterfly" shown in [link] which relates a length-N DFT to one length-N/2 DFT and two length-N/4 DFT's with twiddlefactors. Repeating this process for the half and quarter length DFT's until scalars result gives the SRFFT algorithm in much thesame way the decimation-in-frequency radix-2 Cooley-Tukey FFT is derived [link] , [link] , [link] . The resulting flow graph for the algorithm calculated in place looks like a radix-2 FFT except forthe location of the twiddle factors. Indeed, it is the location of the twiddle factors that makes this algorithm use less arithmetic.The L- shaped SRFFT butterfly [link] advances the calculation of the top half by one of the stages while the lower half, like a radix-4 butterfly, calculates two stages at once. This is illustrated for in [link] .
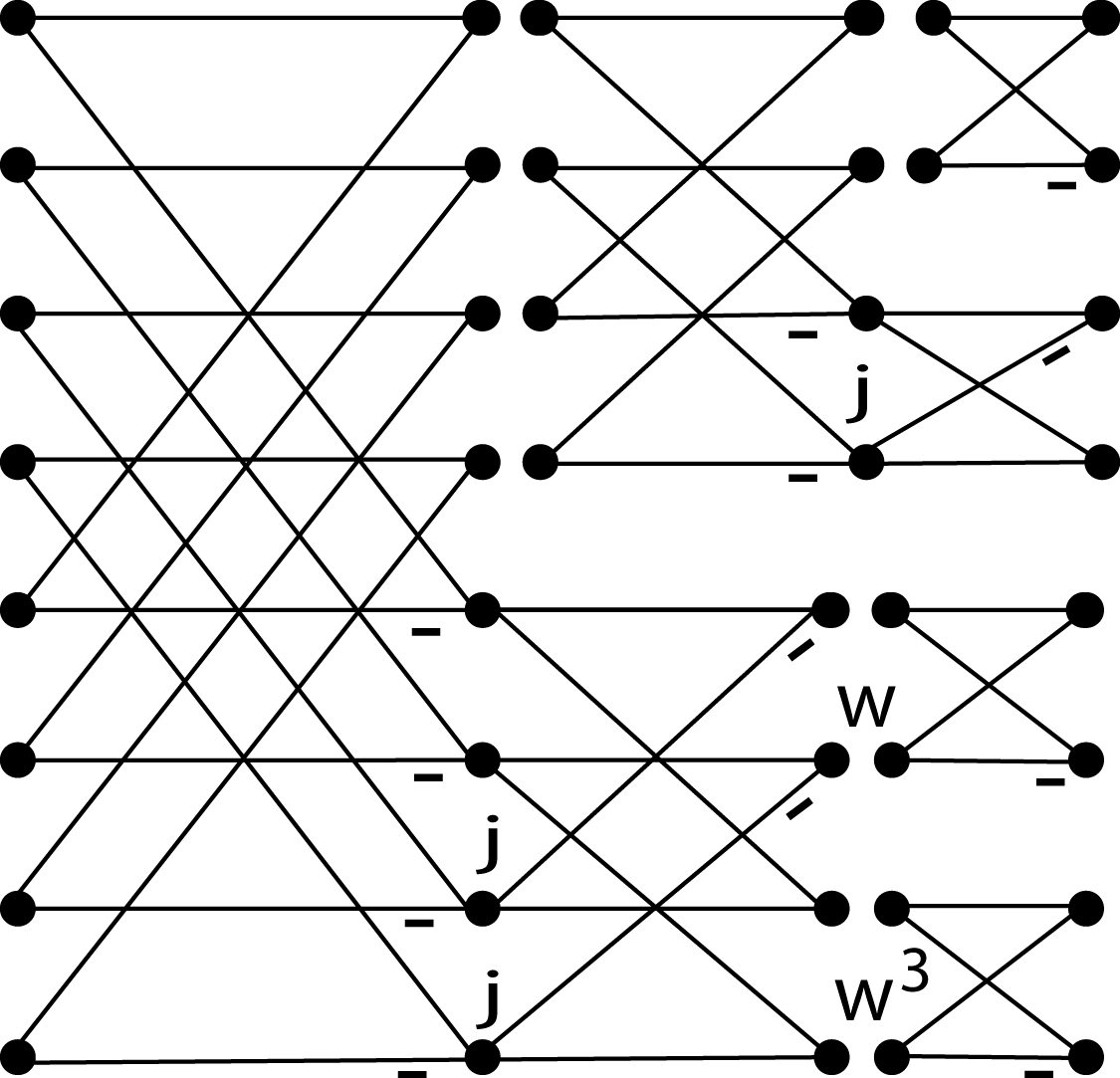
Unlike the fixed radix, mixed radix or variable radix Cooley-Tukey FFT or even the prime factor algorithm or WinogradFourier transform algorithm , the Split-Radix FFT does not progress completely stage by stage, or, in terms of indices, does notcomplete each nested sum in order. This is perhaps better seen from the polynomial formulation of Martens [link] . Because of this, the indexing is somewhat more complicated than theconventional Cooley-Tukey program.
A FORTRAN program is given below which implements the basic decimation-in-frequency split-radix FFT algorithm. The indexingscheme [link] of this program gives a structure very similar to the Cooley-Tukey programs in [link] and allows the same modifications and improvements such as decimation-in-time, multiplebutterflies, table look-up of sine and cosine values, three real per complex multiply methods, and real data versions [link] , [link] .
SUBROUTINE FFT(X,Y,N,M)
N2 = 2*NDO 10 K = 1, M-1
N2 = N2/2N4 = N2/4
E = 6.283185307179586/N2A = 0
DO 20 J = 1, N4A3 = 3*A
CC1 = COS(A)SS1 = SIN(A)
CC3 = COS(A3)SS3 = SIN(A3)
A = J*EIS = J
ID = 2*N240 DO 30 I0 = IS, N-1, ID
I1 = I0 + N4I2 = I1 + N4
I3 = I2 + N4R1 = X(I0) - X(I2)
X(I0) = X(I0) + X(I2)R2 = X(I1) - X(I3)
X(I1) = X(I1) + X(I3)S1 = Y(I0) - Y(I2)
Y(I0) = Y(I0) + Y(I2)S2 = Y(I1) - Y(I3)
Y(I1) = Y(I1) + Y(I3)S3 = R1 - S2
R1 = R1 + S2S2 = R2 - S1
R2 = R2 + S1X(I2) = R1*CC1 - S2*SS1
Y(I2) =-S2*CC1 - R1*SS1X(I3) = S3*CC3 + R2*SS3
Y(I3) = R2*CC3 - S3*SS330 CONTINUE
IS = 2*ID - N2 + JID = 4*ID
IF (IS.LT.N) GOTO 4020 CONTINUE
10 CONTINUEIS = 1
ID = 450 DO 60 I0 = IS, N, ID
I1 = I0 + 1R1 = X(I0)
X(I0) = R1 + X(I1)X(I1) = R1 - X(I1)
R1 = Y(I0)Y(I0) = R1 + Y(I1)
60 Y(I1) = R1 - Y(I1)IS = 2*ID - 1
ID = 4*IDIF (IS.LT.N) GOTO 50
Split-Radix FFT FORTRAN Subroutine

Notification Switch
Would you like to follow the 'Fast fourier transforms' conversation and receive update notifications?