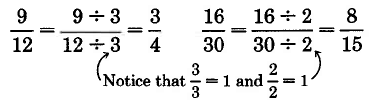1. Home
  2. Contemporary math applications
  3. Exam 1
  4. Fractions
  5. Fractions: equivalent fractions

1.3 Fractions: equivalent fractions

<< Chapter < Page
  Contemporary math applications     Page 1 / 3
Chapter >> Page >
This module is from Fundamentals of Mathematics by Denny Burzynski and Wade Ellis, Jr. This module discusses equivalent fractions, reducing fractions to lowest terms, and raising fractions to higher terms. By the end of the module students should be able to recognize equivalent fractions, reduce a fraction to lowest terms and be able to raise a fraction to higher terms.

Section overview

  • Equivalent Fractions
  • Reducing Fractions to Lowest Terms
  • Raising Fractions to Higher Terms

Equivalent fractions

Let's examine the following two diagrams.

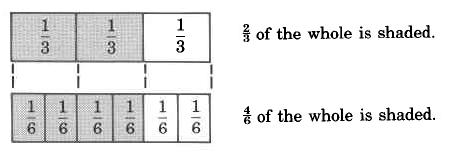
A rectangle divided equally into three parts, each marked one-third. The left two parts are shaded. To the right of the box is the caption, two-thirds of the whole is shaded. Below this is a rectangle equally divided into six part, with the leftmost four part shaded. to the right of this rectangle is the caption, four-sixths of the whole is shaded.

Notice that both 2 3 size 12{ { {2} over {3} } } {} and 4 6 size 12{ { {4} over {6} } } {} represent the same part of the whole, that is, they represent the same number.

Equivalent fractions

Fractions that have the same value are called equivalent fractions . Equiva­lent fractions may look different, but they are still the same point on the number line.

There is an interesting property that equivalent fractions satisfy.

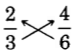
two-thirds and four-sixths, with an arrow from each denominator pointing to the numerator of the opposite fraction.

A test for equivalent fractions using the cross product

These pairs of products are called cross products .

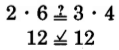
Is two time six equal to three times four? Yes.

If the cross products are equal, the fractions are equivalent. If the cross products are not equal, the fractions are not equivalent.

Thus, 2 3 size 12{ { {2} over {3} } } {} and 4 6 size 12{ { {4} over {6} } } {} are equivalent, that is, 2 3 = 4 6 size 12{ { {2} over {3} } = { {4} over {6} } } {} .

Sample set a

Determine if the following pairs of fractions are equivalent.

3 4 and 6 8 size 12{ { {3} over {4} } `"and " { {6} over {8} } } {} . Test for equality of the cross products.

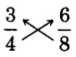
three-fourths and six-eigths, with an arrow from each denominator pointing to the numerator of the opposite fraction.

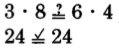Is three times eight equal to six times four? yes. The cross products are equals.

The fractions 3 4 and 6 8 are equivalent, so 3 4 = 6 8 .

3 8 and 9 16 size 12{ { {3} over {8} } " and " { {9} over {"16"} } } {} . Test for equality of the cross products.

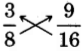
Three-eights and nine-sixteenths, with an arrow from each denominator pointing to the numerator of the opposite fraction.

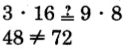is three times sixteen equal to nine times eight? No. forty-eight does not equal seventy-two. The cross products are not equal.

The fractions 3 8 size 12{ { {3} over {8} } } {} and 9 16 size 12{ { {9} over {"16"} } } {} are not equivalent.

Practice set a

Determine if the pairs of fractions are equivalent.

1 2 size 12{ { {1} over {2} } } {} , 3 6 size 12{ { {3} over {6} } } {}

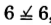Six equals six. , yes

4 5 size 12{ { {4} over {5} } } {} , 12 15 size 12{ { {"12"} over {"15"} } } {}

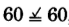Sixty equals sixty. , yes

2 3 size 12{ { {2} over {3} } } {} , 8 15 size 12{ { {8} over {"15"} } } {}

30 ≠ 24 , no

1 8 size 12{ { {1} over {8} } } {} , 5 40 size 12{ { {5} over {"40"} } } {}

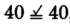Forty equals forty. , yes

3 12 size 12{ { {3} over {"12"} } } {} , 1 4 size 12{ { {1} over {4} } } {}

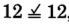Twelve equals twelve. , yes

Reducing fractions to lowest terms

It is often very useful to conver t one fraction to an equivalent fraction that has reduced values in the numerator and denominator. We can suggest a method for doing so by considering the equivalent fractions 9 15 size 12{ { {9} over {"15"} } } {} and 3 5 size 12{ { {3} over {5} } } {} . First, divide both the numerator and denominator of 9 15 size 12{ { {9} over {"15"} } } {} by 3. The fractions 9 15 size 12{ { {9} over {"15"} } } {} and 3 5 size 12{ { {3} over {5} } } {} are equivalent.

(Can you prove this?) So, 9 15 = 3 5 size 12{ { {9} over {"15"} } = { {3} over {5} } } {} . We wish to convert 9 15 size 12{ { {9} over {"15"} } } {} to 3 5 size 12{ { {3} over {5} } } {} . Now divide the numerator and denominator of 9 15 size 12{ { {9} over {"15"} } } {} by 3, and see what happens.

9 ÷ 3 15 ÷ 3 = 3 5 size 12{ { {9 div 3} over {"15" div 3} } = { {3} over {5} } } {}

The fraction 9 15 size 12{ { {9} over {"15"} } } {} is converted to 3 5 size 12{ { {3} over {5} } } {} .

A natural question is "Why did we choose to divide by 3?" Notice that

9 15 = 3 ⋅ 3 5 ⋅ 3 size 12{ { {9} over {"15"} } = { {3 cdot 3} over {5 cdot 3} } } {}

We can see that the factor 3 is common to both the numerator and denominator.

Reducing a fraction

From these observations we can suggest the following method for converting one fraction to an equivalent fraction that has reduced values in the numerator and denominator. The method is called reducing a fraction .

A fraction can be reduced by dividing both the numerator and denominator by the same nonzero whole number.

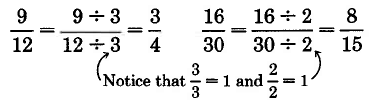
Nine-twelfths is equal to nine divided by three, over nine divided by three, which is equal to three-fourths. Sixteen thirtieths is equal to sixteen divided by two, over thirty divided by 2, which is equal to eight-fifteenths. Notice that three over three and two over two are both equal to 1.

Consider the collection of equivalent fractions

5 20 size 12{ { {5} over {"20"} } } {} , 4 16 size 12{ { {4} over {"16"} } } {} , 3 12 size 12{ { {3} over {"12"} } } {} , 2 8 size 12{ { {2} over {8} } } {} , 1 4 size 12{ { {1} over {4} } } {}

Reduced to lowest terms

Notice that each of the first four fractions can be reduced to the last fraction, 1 4 size 12{ { {1} over {4} } } {} , by dividing both the numerator and denominator by, respectively, 5, 4, 3, and 2. When a fraction is converted to the fraction that has the smallest numerator and denomi­nator in its collection of equivalent fractions, it is said to be reduced to lowest terms . The fractions 1 4 size 12{ { {1} over {4} } } {} , 3 8 size 12{ { {3} over {8} } } {} , 2 5 size 12{ { {2} over {5} } } {} , and 7 10 size 12{ { {7} over {"10"} } } {} are all reduced to lowest terms.

Questions & Answers

prostaglandin and fever
Maha Reply
Discuss the differences between taste and flavor, including how other sensory inputs contribute to our  perception of flavor.
John Reply
taste refers to your understanding of the flavor . while flavor one The other hand is refers to sort of just a blend things.
Faith
While taste primarily relies on our taste buds, flavor involves a complex interplay between taste and aroma
Kamara
which drugs can we use for ulcers
Ummi Reply
omeprazole
Kamara
what
Renee
what is this
Renee
is a drug
Kamara
of anti-ulcer
Kamara
Omeprazole Cimetidine / Tagament For the complicated once ulcer - kit
Patrick
what is the function of lymphatic system
Nency Reply
Not really sure
Eli
to drain extracellular fluid all over the body.
asegid
The lymphatic system plays several crucial roles in the human body, functioning as a key component of the immune system and contributing to the maintenance of fluid balance. Its main functions include: 1. Immune Response: The lymphatic system produces and transports lymphocytes, which are a type of
asegid
to transport fluids fats proteins and lymphocytes to the blood stream as lymph
Adama
what is anatomy
Oyindarmola Reply
Anatomy is the identification and description of the structures of living things
Kamara
what's the difference between anatomy and physiology
Oyerinde Reply
Anatomy is the study of the structure of the body, while physiology is the study of the function of the body. Anatomy looks at the body's organs and systems, while physiology looks at how those organs and systems work together to keep the body functioning.
AI-Robot
what is enzymes all about?
Mohammed Reply
Enzymes are proteins that help speed up chemical reactions in our bodies. Enzymes are essential for digestion, liver function and much more. Too much or too little of a certain enzyme can cause health problems
Kamara
yes
Prince
how does the stomach protect itself from the damaging effects of HCl
Wulku Reply
little girl okay how does the stomach protect itself from the damaging effect of HCL
Wulku
it is because of the enzyme that the stomach produce that help the stomach from the damaging effect of HCL
Kamara
function of digestive system
Ali Reply
function of digestive
Ali
the diagram of the lungs
Adaeze Reply
what is the normal body temperature
Diya Reply
37 degrees selcius
Xolo
37°c
Stephanie
please why 37 degree selcius normal temperature
Mark
36.5
Simon
37°c
Iyogho
the normal temperature is 37°c or 98.6 °Fahrenheit is important for maintaining the homeostasis in the body the body regular this temperature through the process called thermoregulation which involves brain skin muscle and other organ working together to maintain stable internal temperature
Stephanie
37A c
Wulku
what is anaemia
Diya Reply
anaemia is the decrease in RBC count hemoglobin count and PVC count
Eniola
what is the pH of the vagina
Diya Reply
how does Lysin attack pathogens
Diya
acid
Mary
I information on anatomy position and digestive system and there enzyme
Elisha Reply
anatomy of the female external genitalia
Muhammad Reply
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Contemporary math applications. OpenStax CNX. Dec 15, 2014 Download for free at http://legacy.cnx.org/content/col11559/1.6
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Contemporary math applications' conversation and receive update notifications?

Ask