| << Chapter < Page | Chapter >> Page > |
Our research has been devoted to minimizing the -boundary-weighted area of surfaces. We have also studied the boundary-value weighted Dirichlet energy over the interval [0,1]. These two problems have required us to study the minimal surface equation over the plane, using techniques from geometric calculus of variations.
Given a surface we define the -boundary-weighted area of to be
For the disc of radius and the cylinder of radius and height we have:
If then
Problem: Given a curve in does there exist a surface with boundary
disjoint curves so that the -boundary-weighted area of is least amongst all surfaces having boundary at least ?
Consider the upper-half of the truncated catenoid given by the graph of for we have
Let where and We define the -boundary-value weighted Dirichlet energy of a function to be:
We seek to minimize over functions subject to the constraints
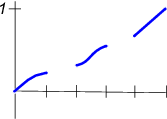
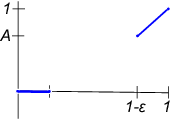
We can show that we only need to consider functions that vanish along the majority of the interval. We therefore need to minimize the function over given by
For a minimizer is with which is unique for When no minimizer exists, but can be approximated by the sequence letting
We define the -boundary-value weighted area of a function to be:
The minimizer for is with unique for When , no minimizer exists.
The MSE in two variables is the PDE:
A function satisfies over the unit disk if and only if the graph of has the least surface area amongst all other graphs of functions with the same boundary values. Solutions to the MSE satisfy the Maximum Principle: if in then attains its max/min only at the boundary, unless if is constant.
is a solution to the MSE for
Our next task is to study the catenoid more closely. We wish to investigate the 2-D versions of the -boundary-value weighted Dirichlet energy and area. The Isoperimetric Inequality states that if is a region bounded by a curve then We need to see how this theory applies.
We thank the guidance offered by our PFUG leader Dr. Leobardo Rosales. We also thank our faculty sponsors in the Department of Mathematics, Dr. Robert Hardt and Dr. Michael Wolf. We also thank the undergraduate group members Sylvia Casas de Leon, James Hart, Marissa Lawson, Conor Loftis, Aneesh Mehta, and Trey Villafane. This work was supported by NSF grant No. DMS-0739420.

Notification Switch
Would you like to follow the 'The art of the pfug' conversation and receive update notifications?