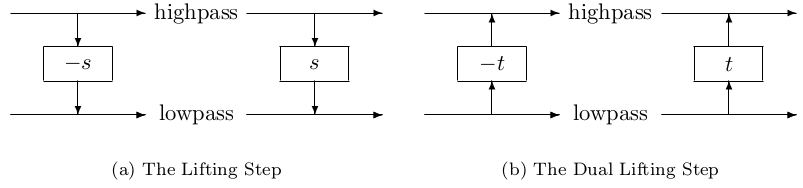
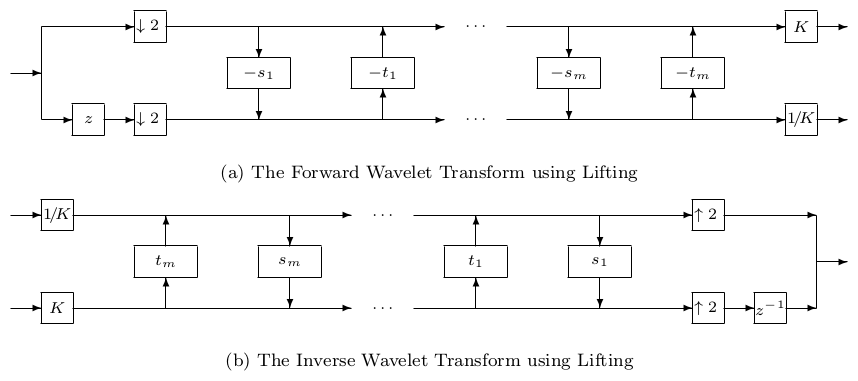
| << Chapter < Page | Chapter >> Page > |
In Chapter: A multiresolution formulation of Wavelet Systems , we introduced the multiresolution analysis for the space of functions, where we have a set of nesting subspaces
where each subspace is spanned by translations of scaled versions of a single scaling function ; e.g.,
The direct difference between nesting subspaces are spanned by translations of asingle wavelet at the corresponding scale; e.g.,
There are several limitations of this construction. For example, nontrivial orthogonal wavelets can not be symmetric. To avoid this problem, we generalizedthe basic construction, and introduced multiplicity- ( -band) scaling functions and wavelets in [link] , where the difference spaces are spanned by translationsof wavelets. The scaling is in terms of the power of ; i.e.,
In general, there are more degrees of freedom to design the M-band wavelets. However, the nested spaces are still spanned by translations of a single scaling function.It is the multiwavelets that removes the above restriction, thus allowing multiple scaling functions to span the nested spaces [link] , [link] , [link] . Although it is possible to construct -band multiwavelets, here we only present results on the two-band case, as most of the researches in theliterature do.
Assume that is spanned by translations of different scaling functions , . For a two-band system, we define the scaling and translation of these functions by
The multiresolution formulation implies
We next construct a vector scaling function by
Since , we have
where is a matrix for each . This is a matrix version of the scalar recursive equation [link] . The first and simplest multiscaling functions probably appear in [link] , and they are shown in [link] .
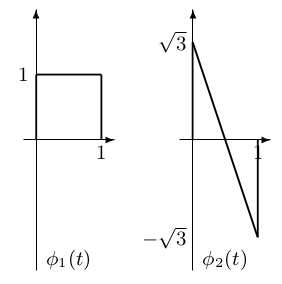
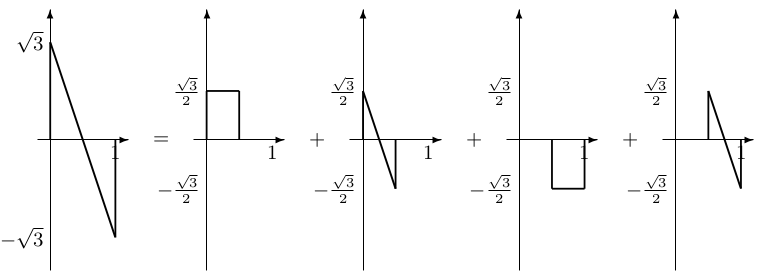
The first scaling function is nothing but the Haar scaling function,and it is the sum of two time-compressed and shifted versions of itself, as shown in [link] (a). The second scaling function can be easilydecomposed into linear combinations of time-compressed and shifted versions of the Haar scaling function and itself, as
This is shown in [link]
Putting the two scaling functions together, we have
Further assume wavelets span the difference spaces; i.e.,
Since for the stacked wavelets there must exist a sequence of matrices , such that
These are vector versions of the two scale recursive equations [link] and [link] .
We can also define the discrete-time Fourier transform of and as
Recall from Chapter: Regularity, Moments, and Wavelet System Design that the key to regularity and smoothness is having enough number of zeros at for . For multiwavelets, it has been shown that polynomials can be exactly reproduced by translatesof if and only if can be factored in special form [link] , [link] , [link] . The factorization is used to study the regularity and convergence of refinablefunction vectors [link] , and to construct multi-scaling functions with approximation and symmetry [link] . Approximation and smoothness of multiple refinable functions are also studied in [link] , [link] , [link] .

Notification Switch
Would you like to follow the 'Wavelets and wavelet transforms' conversation and receive update notifications?