2.2 Vectors in three dimensions  (Page 6/14)

Throwing a forward pass

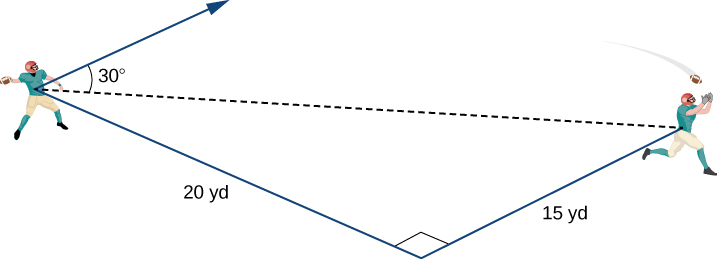
A quarterback is standing on the football field preparing to throw a pass. His receiver is standing 20 yd down the field and 15 yd to the quarterback’s left. The quarterback throws the ball at a velocity of 60 mph toward the receiver at an upward angle of $30\text{°}$ (see the following figure). Write the initial velocity vector of the ball, $\text{v},$ in component form.

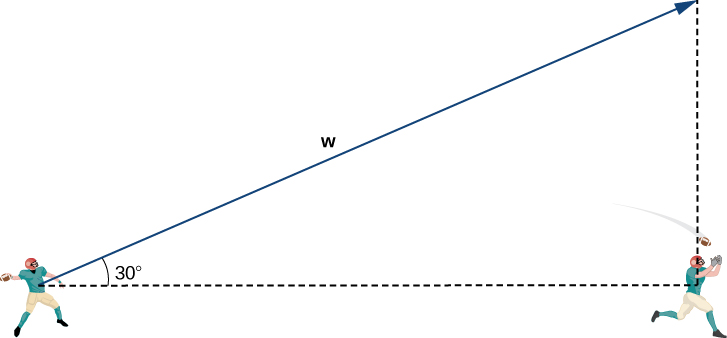
The first thing we want to do is find a vector in the same direction as the velocity vector of the ball. We then scale the vector appropriately so that it has the right magnitude. Consider the vector $\text{w}$ extending from the quarterback’s arm to a point directly above the receiver’s head at an angle of $30\text{°}$ (see the following figure). This vector would have the same direction as $\text{v},$ but it may not have the right magnitude.

The receiver is 20 yd down the field and 15 yd to the quarterback’s left. Therefore, the straight-line distance from the quarterback to the receiver is

$\text{Dist from QB to receiver}=\sqrt{{15}^2+{20}^2}=\sqrt{225+400}=\sqrt{625}=25\text{yd}.$

We have $\frac{25}{\Vert \text{w}\Vert }=\text{cos}30\text{°}.$ Then the magnitude of $\text{w}$ is given by

$\Vert \text{w}\Vert =\frac{25}{\text{cos}30\text{°}}=\frac{25·2}{\sqrt{3}}=\frac{50}{\sqrt{3}}\text{yd}$

and the vertical distance from the receiver to the terminal point of $\text{w}$ is

$\text{Vert dist from receiver to terminal point of}\text{w}=\Vert \text{w}\Vert \text{sin}30\text{°}=\frac{50}{\sqrt{3}}·\frac{1}{2}=\frac{25}{\sqrt{3}}\text{yd}.$

Then $\text{w}=⟨20,15,\frac{25}{\sqrt{3}}⟩,$ and has the same direction as $\text{v}.$

Recall, though, that we calculated the magnitude of $\text{w}$ to be $\Vert \text{w}\Vert =\frac{50}{\sqrt{3}},$ and $\text{v}$ has magnitude $60$ mph. So, we need to multiply vector $\text{w}$ by an appropriate constant, $k.$ We want to find a value of $k$ so that $\Vert k\text{w}\Vert =60$ mph. We have

$\Vert k\text{w}\Vert =k\Vert \text{w}\Vert =k\frac{50}{\sqrt{3}}\text{mph,}$

so we want

$\begin{array}{}\\ \\ \hfill k\frac{50}{\sqrt{3}}& =\hfill & 60\hfill \\ \hfill k& =\hfill & \frac{60\sqrt{3}}{50}\hfill \\ \hfill k& =\hfill & \frac{6\sqrt{3}}{5}.\hfill \end{array}$

Then

$\text{v}=k\text{w}=k⟨20,15,\frac{25}{\sqrt{3}}⟩=\frac{6\sqrt{3}}{5}⟨20,15,\frac{25}{\sqrt{3}}⟩=⟨24\sqrt{3},18\sqrt{3},30⟩.$

Let’s double-check that $\Vert \text{v}\Vert =60.$ We have

$\Vert \text{v}\Vert =\sqrt{{\left(24\sqrt{3}\right)}^2+{\left(18\sqrt{3}\right)}^2+{\left(30\right)}^2}=\sqrt{1728+972+900}=\sqrt{3600}=60\text{mph}.$

So, we have found the correct components for $\text{v}.$

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Key concepts

• The three-dimensional coordinate system is built around a set of three axes that intersect at right angles at a single point, the origin. Ordered triples $\left(x,y,z\right)$ are used to describe the location of a point in space.
• The distance $d$ between points $\left(x_1,y_1,z_1\right)$ and $\left(x_2,y_2,z_2\right)$ is given by the formula
  
  $d=\sqrt{{\left(x_2-x_1\right)}^2+{\left(y_2-y_1\right)}^2+{\left(z_2-z_1\right)}^2}.$
• In three dimensions, the equations $x=a,y=b,\text{and}z=c$ describe planes that are parallel to the coordinate planes.
• The standard equation of a sphere with center $\left(a,b,c\right)$ and radius $r$ is
  
  ${\left(x-a\right)}^2+{\left(y-b\right)}^2+{\left(z-c\right)}^2=r^2.$
• In three dimensions, as in two, vectors are commonly expressed in component form, $\text{v}=⟨x,y,z⟩,$ or in terms of the standard unit vectors, $x\text{i}+y\text{j}+z\text{k}.$
• Properties of vectors in space are a natural extension of the properties for vectors in a plane. Let $\text{v}=⟨x_1,y_1,z_1⟩$ and $\text{w}=⟨x_2,y_2,z_2⟩$ be vectors, and let $k$ be a scalar.
  • Scalar multiplication: $k\text{v}=⟨k{x}_1,k{y}_1,k{z}_1⟩$
  • Vector addition: $\text{v}+\text{w}=⟨x_1,y_1,z_1⟩+⟨x_2,y_2,z_2⟩=⟨x_1+x_2,y_1+y_2,z_1+z_2⟩$
  • Vector subtraction: $\text{v}-\text{w}=⟨x_1,y_1,z_1⟩-⟨x_2,y_2,z_2⟩=⟨x_1-x_2,y_1-y_2,z_1-z_2⟩$
  • Vector magnitude: $\Vert \text{v}\Vert =\sqrt{x_1{}^2+y_1{}^2+z_1{}^2}$
  • Unit vector in the direction of v: $\frac{\text{v}}{\Vert \text{v}\Vert }=\frac{1}{\Vert \text{v}\Vert }⟨x_1,y_1,z_1⟩=⟨\frac{x_1}{\Vert \text{v}\Vert },\frac{y_1}{\Vert \text{v}\Vert },\frac{z_1}{\Vert \text{v}\Vert }⟩,$ $\text{v}\ne 0$