5.7 Change of variables in multiple integrals (Page 6/13)

Calculus volume 3 Page 6 / 13

Let’s try another example with a different substitution.

Evaluating a triple integral with a change of variables

Evaluate the triple integral

\int_{0}^{3} \int_{0}^{4} \int_{y / 2}^{(y / 2) + 1} (x + \frac{z}{3}) d x d y d z

in $x y z -space$ by using the transformation

u = (2 x - y) / 2, v = y / 2, and w = z / 3 .

Then integrate over an appropriate region in $u v w -space .$

As before, some kind of sketch of the region $G$ in $x y z -space$ over which we have to perform the integration can help identify the region $D$ in $u v w -space$ ( [link] ). Clearly $G$ in $x y z -space$ is bounded by the planes $x = y / 2, x = (y / 2) + 1, y = 0,$ $y = 4,$ $z = 0, and z = 4 .$ We also know that we have to use $u = (2 x - y) / 2, v = y / 2, and w = z / 3$ for the transformations. We need to solve for $x, y, and z .$ Here we find that $x = u + v,$ $y = 2 v,$ and $z = 3 w .$

Using elementary algebra, we can find the corresponding surfaces for the region $G$ and the limits of integration in $u v w -space .$ It is convenient to list these equations in a table.

Equations in $x y z$ for the region $D$	Corresponding equations in $u v w$ for the region $G$	Limits for the integration in $u v w$
$x = y / 2$	$u + v = 2 v / 2 = v$	$u = 0$
$x = y / 2$	$u + v = (2 v / 2) + 1 = v + 1$	$u = 1$
$y = 0$	$2 v = 0$	$v = 0$
$y = 4$	$2 v = 4$	$v = 2$
$z = 0$	$3 w = 0$	$w = 0$
$z = 3$	$3 w = 3$	$w = 1$

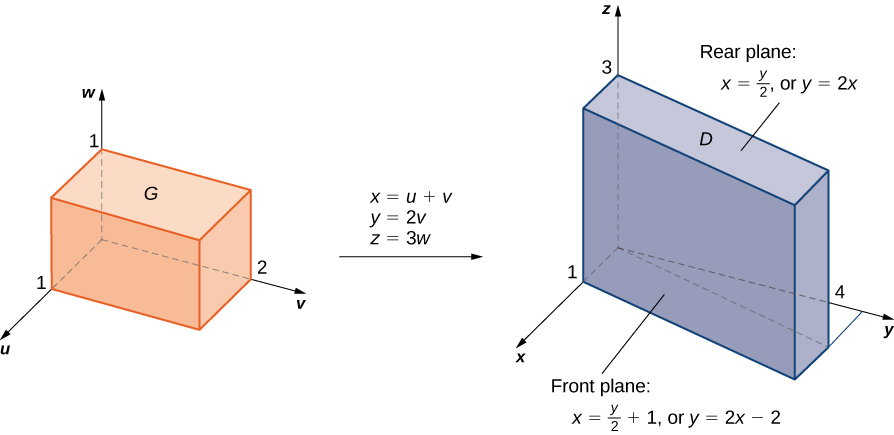
On the left-hand side of this figure, there is a box G with sides 1, 2, and 1 along the u, v, and w axes, respectively. Then there is an arrow from this graph to the right-hand side of the figure marked with x = u + v, y = 2v, and z = 3w. On the right-hand side of this figure there is a region D in xyz space that is a rotated box with sides 1, 4, and 3 along the x, y, and z axes. The rear plane is marked x = y/2 or y = 2x. The front plane is marked x = y/2 + 1 or y = 2x minus 2. — The region $G$ in $u v w -space$ is transformed to region $D$ in $x y z -space .$

Now we can calculate the Jacobian for the transformation:

J (u, v, w) = | \begin{matrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} & \frac{\partial y}{\partial w} \\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} & \frac{\partial z}{\partial w} \end{matrix} | = | \begin{matrix} 1 & 1 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{matrix} | = 6 .

The function to be integrated becomes

f (x, y, z) = x + \frac{z}{3} = u + v + \frac{3 w}{3} = u + v + w .

We are now ready to put everything together and complete the problem.

\begin{matrix} \int_{0}^{3} \int_{0}^{4} \int_{y / 2}^{(y / 2) + 1} (x + \frac{z}{3}) d x d y d z \\ = \int_{0}^{1} \int_{0}^{2} \int_{0}^{1} (u + v + w) | J (u, v, w) | d u d v d w = \int_{0}^{1} \int_{0}^{2} \int_{0}^{1} (u + v + w) | 6 | d u d v d w \\ = 6 \int_{0}^{1} \int_{0}^{2} \int_{0}^{1} (u + v + w) d u d v d w = 6 {\int_{0}^{1} \int_{0}^{2} [\frac{u^{2}}{2} + v u + w u]}_{0}^{1} d v d w \\ = 6 \int_{0}^{1} \int_{0}^{2} (\frac{1}{2} + v + w) d v d w = 6 {\int_{0}^{1} [\frac{1}{2} v + \frac{v^{2}}{2} + w v]}_{0}^{2} d w \\ = 6 \int_{0}^{1} (3 + 2 w) d w = 6 {[3 w + w^{2}]}_{0}^{1} = 24. \end{matrix}

Got questions? Get instant answers now!

Let $D$ be the region in $x y z -space$ defined by $1 \leq x \leq 2, 0 \leq x y \leq 2, and 0 \leq z \leq 1 .$

Evaluate $\underset{D}{∭} (x^{2} y + 3 x y z) d x d y d z$ by using the transformation $u = x, v = x y,$ and $w = 3 z .$

$\int_{0}^{3} \int_{0}^{2} \int_{1}^{2} (\frac{v}{3} + \frac{v w}{3 u}) d u d v d w = 2 + ln 8$

Got questions? Get instant answers now!

Key concepts

A transformation $T$ is a function that transforms a region $G$ in one plane (space) into a region $R$ in another plane (space) by a change of variables.
A transformation $T : G \to R$ defined as $T (u, v) = (x, y)$ $(or T (u, v, w) = (x, y, z))$ is said to be a one-to-one transformation if no two points map to the same image point.
If $f$ is continuous on $R,$ then $\iint_{R} f (x, y) d A = \iint_{S} f (g (u, v), h (u, v)) | \frac{\partial (x, y)}{\partial (u, v)} | d u d v .$
If $F$ is continuous on $R,$ then

$\begin{matrix} \underset{R}{∭} F (x, y, z) d V & = \underset{G}{∭} F (g (u, v, w), h (u, v, w), k (u, v, w)) | \frac{\partial (x, y, z)}{\partial (u, v, w)} | d u d v d w \\ = \underset{G}{∭} H (u, v, w) | J (u, v, w) | d u d v d w . \end{matrix}$

In the following exercises, the function $T : S \to R, T (u, v) = (x, y)$ on the region $S = {(u, v) | 0 \leq u \leq 1, 0 \leq v \leq 1}$ bounded by the unit square is given, where $R \subset R^{2}$ is the image of $S$ under $T .$

Justify that the function $T$ is a $C^{1}$ transformation.
Find the images of the vertices of the unit square $S$ through the function $T .$
Determine the image $R$ of the unit square $S$ and graph it.

$x = 2 u, y = 3 v$

Got questions? Get instant answers now!

$x = \frac{u}{2}, y = \frac{v}{3}$

a. $T (u, v) = (g (u, v), h (u, v)), x = g (u, v) = \frac{u}{2}$ and $y = h (u, v) = \frac{v}{3} .$ The functions $g$ and $h$ are continuous and differentiable, and the partial derivatives $g_{u} (u, v) = \frac{1}{2},$ $g_{v} (u, v) = 0, h_{u} (u, v) = 0 and h_{v} (u, v) = \frac{1}{3}$ are continuous on $S;$ b. $T (0, 0) = (0, 0),$ $T (1, 0) = (\frac{1}{2}, 0), T (0, 1) = (0, \frac{1}{3}),$ and $T (1, 1) = (\frac{1}{2}, \frac{1}{3});$ c. 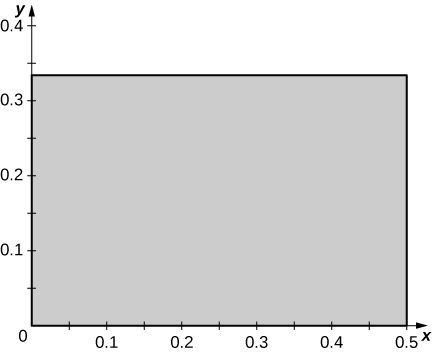$R$ is the rectangle of vertices $(0, 0), (\frac{1}{2}, 0), (\frac{1}{2}, \frac{1}{3}), and (0, \frac{1}{3})$ in the $x y -plane;$ the following figure.
A rectangle with one corner at the origin, horizontal length 0.5, and vertical height 0.34.

Got questions? Get instant answers now!

$x = u - v, y = u + v$

Got questions? Get instant answers now!

$x = 2 u - v, y = u + 2 v$

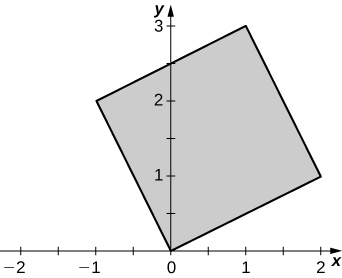
a. $T (u, v) = (g (u, v), h (u, v)), x = g (u, v) = 2 u - v,$ and $y = h (u, v) = u + 2 v .$ The functions $g$ and $h$ are continuous and differentiable, and the partial derivatives $g_{u} (u, v) = 2,$ $g_{v} (u, v) = −1,$ $h_{u} (u, v) = 1,$ and $h_{v} (u, v) = 2$ are continuous on $S;$ b. $T (0, 0) = (0, 0),$ $T (1, 0) = (2, 1),$ $T (0, 1) = (−1, 2),$ and $T (1, 1) = (1, 3);$ c. $R$ is the parallelogram of vertices $(0, 0), (2, 1), (1, 3), and (−1, 2)$ in the $x y -plane;$ see the following figure.
A square of side length square root of 5 with one corner at the origin and another at (2, 1).

Got questions? Get instant answers now!

Questions & Answers

calculate molarity of NaOH solution when 25.0ml of NaOH titrated with 27.2ml of 0.2m H2SO4

Gasin Reply

what's Thermochemistry

rhoda Reply

the study of the heat energy which is associated with chemical reactions

Kaddija

How was CH4 and o2 was able to produce (Co2)and (H2o

Edafe Reply

explain please

Victory

First twenty elements with their valences

Martine Reply

what is chemistry

asue Reply

what is atom

asue

what is the best way to define periodic table for jamb

Damilola Reply

what is the change of matter from one state to another

Elijah Reply

what is isolation of organic compounds

IKyernum Reply

what is atomic radius

ThankGod Reply

Read Chapter 6, section 5

Kareem

Atomic radius is the radius of the atom and is also called the orbital radius

Kareem

atomic radius is the distance between the nucleus of an atom and its valence shell

Amos

Read Chapter 6, section 5

paulino

Bohr's model of the theory atom

Ayom Reply

is there a question?

when a gas is compressed why it becomes hot?

ATOMIC

It has no oxygen then

Goldyei

read the chapter on thermochemistry...the sections on "PV" work and the First Law of Thermodynamics should help..

Which element react with water

Mukthar Reply

Mgo

Ibeh

an increase in the pressure of a gas results in the decrease of its

Valentina Reply

definition of the periodic table

Cosmos Reply

What is the lkenes

Da Reply

what were atoms composed of?

Moses Reply

Got questions? Join the online conversation and get instant answers!

Jobilize.com Reply

<< Chapter < Page Page > Chapter >>

Practice Key Terms 4

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?

Ask

	Financial Intelligence Quiz By Yasser Ibrahim Start Quiz
	Real Estate Finance Exam 2003 By Tod McGrath Start Exam
	7 Java Messaging Service By JavaChamp Team Start Quiz
	6 Sociology 06 Groups and Organization MCQ By OpenStax Start Quiz
	Foundations of Software Engineering By Kevin Amaratunga Start Quiz
	13 AP Key Terms 13 Anatomy of the Nervous System By OpenStax Start Key Terms
©flickr:	Word Roots and Prefixes By Ellie Banfield Start Quiz
	3 Lec:3 Cohort Studies By Janet Forrester Start Quiz
	18 AP Key Terms 18 Cardiovascular System Blood By OpenStax Start Key Terms
©flickr: Hey	Anatomy Physiology Final By Joli Julianna Start Test