8.9 Dividing polynomials

Overview

• Dividing a Polynomial by a Monomial
• The Process of Division
• Review of Subtraction of Polynomials
• Dividing a Polynomial by a Polynomial

Dividing a polynomial by a monomial

The following examples illustrate how to divide a polynomial by a monomial. The division process is quite simple and is based on addition of rational expressions.

$\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}$

Turning this equation around we get

$\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}$

Now we simply divide $c$ into $a$ , and $c$ into $b$ . This should suggest a rule.

Dividing a polynomial by a monomial

Sample set a

Practice set a

Perform the following divisions.

The process of division

In Section [link] we studied the method of reducing rational expressions. For example, we observed how to reduce an expression such as

$\frac{x^2-2x-8}{x^2-3x-4}$

Our method was to factor both the numerator and denominator, then divide out common factors.

$\frac{\left(x-4\right)\left(x+2\right)}{\left(x-4\right)\left(x+1\right)}$

$\frac{\cancel{\left(x-4\right)}\left(x+2\right)}{\cancel{\left(x-4\right)}\left(x+1\right)}$

$\frac{x+2}{x+1}$

When the numerator and denominator have no factors in common, the division may still occur, but the process is a little more involved than merely factoring. The method of dividing one polynomial by another is much the same as that of dividing one number by another. First, we’ll review the steps in dividing numbers.

1. $\frac{35}{8}.$  We are to divide 35 by 8.
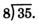2.   We try 4, since 32 divided by 8 is 4.
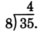3. Multiply 4 and 8.
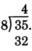4. Subtract 32 from 35.
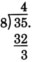5. Since the remainder 3 is less than the divisor 8, we are done with the 32 division.
6. $4\frac{3}{8}.$   The quotient is expressed as a mixed number.