| << Chapter < Page | Chapter >> Page > |
Solution for (a)
The first ball bounces directly into the wall and exerts a force on it in the direction. Therefore the wall exerts a force on the ball in the direction. The second ball continues with the same momentum component in the direction, but reverses its -component of momentum, as seen by sketching a diagram of the angles involved and keeping in mind the proportionality between velocity and momentum.
These changes mean the change in momentum for both balls is in the direction, so the force of the wall on each ball is along the direction.
Strategy for (b)
Calculate the change in momentum for each ball, which is equal to the impulse imparted to the ball.
Solution for (b)
Let be the speed of each ball before and after collision with the wall, and the mass of each ball. Choose the -axis and -axis as previously described, and consider the change in momentum of the first ball which strikes perpendicular to the wall.
Impulse is the change in momentum vector. Therefore the -component of impulse is equal to and the -component of impulse is equal to zero.
Now consider the change in momentum of the second ball.
It should be noted here that while changes sign after the collision, does not. Therefore the -component of impulse is equal to and the -component of impulse is equal to zero.
The ratio of the magnitudes of the impulse imparted to the balls is
Discussion
The direction of impulse and force is the same as in the case of (a); it is normal to the wall and along the negative - direction. Making use of Newton’s third law, the force on the wall due to each ball is normal to the wall along the positive -direction.
Our definition of impulse includes an assumption that the force is constant over the time interval . Forces are usually not constant . Forces vary considerably even during the brief time intervals considered. It is, however, possible to find an average effective force that produces the same result as the corresponding time-varying force. [link] shows a graph of what an actual force looks like as a function of time for a ball bouncing off the floor. The area under the curve has units of momentum and is equal to the impulse or change in momentum between times and . That area is equal to the area inside the rectangle bounded by , , and . Thus the impulses and their effects are the same for both the actual and effective forces.
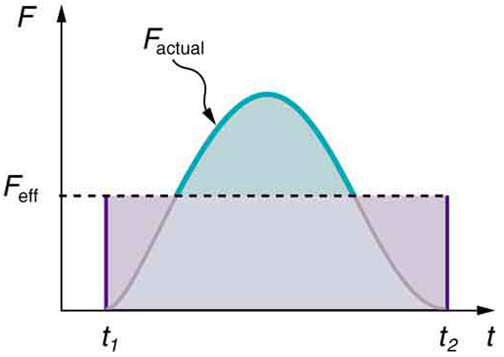
The assumption of a constant force in the definition of impulse is analogous to the assumption of a constant acceleration in kinematics. In both cases, nature is adequately described without the use of calculus.
Professional Application
Explain in terms of impulse how padding reduces forces in a collision. State this in terms of a real example, such as the advantages of a carpeted vs. tile floor for a day care center.
A bullet is accelerated down the barrel of a gun by hot gases produced in the combustion of gun powder. What is the average force exerted on a 0.0300-kg bullet to accelerate it to a speed of 600 m/s in a time of 2.00 ms (milliseconds)?
Professional Application
A car moving at 10 m/s crashes into a tree and stops in 0.26 s. Calculate the force the seat belt exerts on a passenger in the car to bring him to a halt. The mass of the passenger is 70 kg.
Professional Application
A professional boxer hits his opponent with a 1000-N horizontal blow that lasts for 0.150 s. (a) Calculate the impulse imparted by this blow. (b) What is the opponent’s final velocity, if his mass is 105 kg and he is motionless in midair when struck near his center of mass? (c) Calculate the recoil velocity of the opponent’s 10.0-kg head if hit in this manner, assuming the head does not initially transfer significant momentum to the boxer’s body. (d) Discuss the implications of your answers for parts (b) and (c).
Professional Application
One hazard of space travel is debris left by previous missions. There are several thousand objects orbiting Earth that are large enough to be detected by radar, but there are far greater numbers of very small objects, such as flakes of paint. Calculate the force exerted by a 0.100-mg chip of paint that strikes a spacecraft window at a relative speed of , given the collision lasts .
Professional Application
A 75.0-kg person is riding in a car moving at 20.0 m/s when the car runs into a bridge abutment. (a) Calculate the average force on the person if he is stopped by a padded dashboard that compresses an average of 1.00 cm. (b) Calculate the average force on the person if he is stopped by an air bag that compresses an average of 15.0 cm.
(a) away from the dashboard
(b) away from the dashboard
A cruise ship with a mass of strikes a pier at a speed of 0.750 m/s. It comes to rest 6.00 m later, damaging the ship, the pier, and the tugboat captain’s finances. Calculate the average force exerted on the pier using the concept of impulse. (Hint: First calculate the time it took to bring the ship to rest.)
in the boat’s original direction of motion
A 0.450-kg hammer is moving horizontally at 7.00 m/s when it strikes a nail and comes to rest after driving the nail 1.00 cm into a board. (a) Calculate the duration of the impact. (b) What was the average force exerted on the nail?
When serving a tennis ball, a player hits the ball when its velocity is zero (at the highest point of a vertical toss). The racquet exerts a force of 540 N on the ball for 5.00 ms, giving it a final velocity of 45.0 m/s. Using these data, find the mass of the ball.
60.0 g

Notification Switch
Would you like to follow the 'Unit 6 - momentum' conversation and receive update notifications?