| << Chapter < Page | Chapter >> Page > |
Wanneer ons die skoolgebou so bekyk, sien ons dat dit nogal baie verskillend lyk vanaf elkeen van hierdie posisies.
2. Bou die voorwerpe wat hier onder geteken is uit suikerblokkies en kyk dan vanuit verskillende hoeke na hulle.
3. Bou nog 'n paar voorwerpe met suikerblokkies en ondersoek hulle van die voorkant, van agter, van die kante en van die hoeke af.
4. Nou moet julle die voorwerpe wat volg, teken. Teken hulle soos julle hulle sien as julle volgens die instruksies hier onder na hulle kyk:
4.1 van agter
 |
| Voor |

Voor
4.3 vanaf die regterhoek
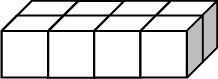
Voor
Aktiwiteit 4:
Om die volume van driedimensionele voorwerpe te ondersoek en te skat [LU 4.8]
1. Pak die vuurhoutjiedosie vol suikerblokkies. Hoeveel blokkies het jy nodig gehad?
2. Doen nou dieselfde met die ander kartondose en voltooi die tabel hier onder:
| Voorwerp (kartondoos) | Aantal suikerblokkies wat nodig was om die kartondosie te vul |
| Vuurhoutjiedosie | |
3. Meet die suikerblokkie en skryf jou bevindings neer:
4. Die vuurhoutjiedosie kan ………… kubusse hou; dus sê ons dat die kartondosie se volume nagenoeg …… kubieke sentimeters is.
5. Wanneer ons meet hoeveel van iets in die spasie in 'n houer kan pas, meet ons die houer se VOLUME; daarvoor het ons drie mate nodig: lengte; breedte en hoogte.
6. Kan jy aan 'n vinniger manier dink as om elke suikerblokkie te meet wanneer jy die volume van 'n houer wil bereken? Bespreek dit met 'n maat en skryf dan jou antwoord op die stippellyn.
7. Hoeveel suikerblokkies sal jy nodig hê om 'n kartondoos wat 20 cm lank; 15 cm breed en 7 cm hoog is (soos 'n 2-liter roomysbak) vol te maak? Skryf jou berekeninge neer en vergelyk hulle dan met dié van 'n maat.
| Leeruitkomstes(LUs) |
| LU 2 |
| Patrone, Funksies en AlgebraDie leerder is in staat om patrone en verwantskappe te herken, te beskryf en voor te stel en probleme op te los deur algebraïese taal en vaardighede te gebruik. |
| Assesseringstandaarde(ASe) |
| Dit is duidelik wanneer die leerder: |
| 2.1 meetkundige patrone ondersoek en uitbrei om verwantskappe of reëls te vind, insluitend patrone soos die volgende: |
|
|
| LU 3 |
| Ruimte en VormDie leerder is in staat om eienskappe en verwantskappe tussen tweedimensionele vorms en driedimensionele voorwerpe in 'n verskeidenheid oriëntasies en posisies te beskryf en voor te stel. |
| Dit is duidelik wanneer die leerder: |
3.2 tweedimensionele vorms en driedimensionele voorwerpe uit die omgewing volgens meetkundige eienskappe beskryf, sorteer en vergelyk, insluitend:
|
| 3.3 tweedimensionele vorms en driedimensionele voorwerpe wat in hierdie graad bestudeer word ondersoek en vergelyk (alleen en/of as ‘n lid van ‘n groep of span) volgens die bostaande eienskappe deur die volgende te doen: |
|
|
| 3.4 die simmetrie-lyne in tweedimensionele vorms, insluitend dié wat in die natuur en in kulturele kunsvorms voorkom, herken en beskryf; |
| 3.5 tweedimensionele vorms, driedimensionele voorwerpe en patrone van meetkundige voorwerpe en vorms (bv. tangramme) met die klem op teëling (tessellasie) en lynsimmetrie skep; |
| 3.6 natuurlike en kulturele tweedimensionele vorms en driedimensionele voorwerpe en patrone na aanleiding van meetkundige eienskappe herken en beskryf; |
| 3.7 die verskille in die voorkoms van 'n voorwerp wat in verskillende posisies gehou word, beskryf; |
| LU 4 |
| MetingDie leerder is in staat om gepaste meeteenhede, instrumente en formules in ‘n verskeidenheid kontekste te gebruik. |
| Dit is duidelik wanneer die leerder: |
| 4.8 ondersoek instel en bepaal by benadering (alleen en/of as lid van 'n groep of span) met betrekking tot: |
4.8.2 oppervlakte van veelhoeke (m.b.v. vierkantroosters en teëling) ten einde ‘n begrip van vierkante eenhede te ontwikkel;
|
AKTIWITEIT 1: 3D voorwerpe
1. Ondersoek - prakties
2. Gebruik 'n ruitenet - prakties
3. Prakties – Tetraëder / viervlak (tetra – Grieks = 4)
4. Gebruik van ondersoeke
| Voorwerp | Vlakke | Plat of gerond | Hoeke | Kante |
| Reghoekige prisma | 6 | Plat | 8 | 12 |
| Kubus | 6 | Plat | 8 | 12 |
| Tetraëder | 4 | Plat | 5 | 7 |
AKTIWITEIT 2: simmetrie
1. PROJEK – eie – prakties
2. Fatsoene
2.1 en 2.2 en 2.3 Knip, vou en trek van simmetrielyne
bv.




( Let wel: skuinslyne (diagonale) in 'n reghoek word nie net vir vou gebruik nie.)
AKTIWITEIT 3: voorwerpe wat vanuit verskillende hoeke gesien word
1.1 tot 1.4 Prakties – bestudeer 'n gebou vanaf verskillende hoeke
2. en 3. Prakties – werk met kubusse
4.1 tot 4.3 Teken – Moeilik!
2.2 (b)
AKTIWITEIT 4: volume
1. eie
2. eie ondersoek
3. 1 cm; 1 cm; 1 cm
4. eie
5. -
6. Bespreking (lengte x breedte x hoogte)
7. 2 100 suikerblokkies

Notification Switch
Would you like to follow the 'Wiskunde graad 4' conversation and receive update notifications?