| << Chapter < Page | Chapter >> Page > |
4a(2a + 1) = 8a + 4a
–5a(2a + 1) = –10a 2 – 5a
a 2 (–3a 2 – 2a) = –3a 4 – 2a 3
–7a(2a – 3) = –14a 2 + 21a
Let op : Ons het ‘n uitdrukking met faktore verander na ‘n uitdrukking met terme . Ons kan ook sê: ‘n P rodukuitdrukking is nou ‘n somuitdrukking .
Oefening:
1. 3x (2x + 4)
C Eenterm × drieterm
5a(5 + 2a – a 2 ) = 25a + 10a 2 – 5a 3
– ½ (10x 5 + 2a 4 – 8a 3 ) = – 5x 5 – a 4 +4a 3
Oefening:
Probeer: 4. 4x (5 – 2x + 4x 2 – 3x 3 + x 4 )
D Tweeterm × tweeterm
Elke term van die eerste tweeterm word vermenigvuldig met elke term van die tweede tweeterm.
(3x + 2) (5x + 4) = (3x)(5x) + (3x)(4) + (2)(5x) + (2)(4) = 15x 2 + 12x + 10x + 8
= 15x 2 + 22x + 8 Maak altyd seker dat jou antwoord vereenvoudig is.
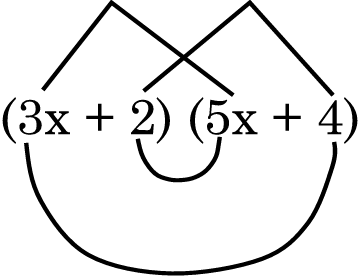
Daar is belangrike patrone in die volgende vermenigvuldigingsoefening – let baie mooi op na hulle.
Oefening:
E Tweeterm × veelterm
(2a + 3) (a 3 – 3a 2 + 2a – 3) = 2a 4 – 6a 3 + 4a 2 – 6a + 3a 3 – 9a 2 + 6a – 9
= 2a 4 – 3a 3 – 5a 2 – 9 (vereenvoudigde vorm)
Oefening:
A Faktore
Hierdie tabel toon die faktore van sekere eenterme.
| Uitdrukking | Kleinste faktore |
| 42 | 2 × 3 × 7 |
| 6ab | 2 × 3 × a × b |
| 21a 2 b | 3 × 7 × a × a × b |
| (5abc 2 ) 2 | 5 × a × b × c × c × 5 × a × b × c × c |
| –8y 4 | –2 × 2 × 2 × y × y × y × y |
| (–8y 4 ) 2 | –2 × 2 × 2 × y × y × y × y × –2 × 2 × 2 × y × y × y × y |
Die faktore kan in enige orde geskryf word, maar as jy by die gebruiklike orde hou, sal jou werk vergemaklik word Twee van die lyste faktore in die tabel is nie in die gebruiklike orde nie – herskryf hulle in orde.
B Gemene faktore van tweeterme
6ab = 3a × 2b en 3ac = 3a × c
6ab + 3ac = 3a (2b + c).

Notification Switch
Would you like to follow the 'Wiskunde graad 9' conversation and receive update notifications?