| << Chapter < Page | Chapter >> Page > |
Suppose the transition matrix for the tennis player in [link] is as follows, where denotes the cross-court shots and denotes down-the-line shots.
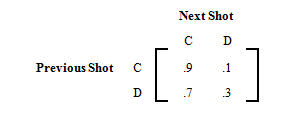
Find the following.
If the player hit the first shot cross-court, what is the probability he will hit the fourth shot cross-court?
Determine the long term shot distribution.
Professor Hay never orders eggs two days in a row, but if he orders tofu one day, then there is an equal probability that he will order tofu or eggs the next day.
Find the following:
If Professor Hay had eggs on Monday, what is the probability that he will have tofu on Friday?
Find the long term distribution for breakfast choices for Professor Hay.
Many Russians have experienced a sharp decline in their living standards due to President Yeltsin's reforms. As a result, in the parliamentary elections held in December 1995, Communists and Nationalists made significant gains, and a new pattern in switching political parties emerged. The transition matrix for such a change is given below, where Communists, Nationalists, and Reformists are denoted by the letters , , and , respectively.
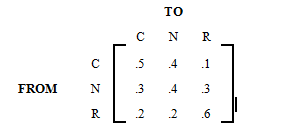
Find the following.
If in this election Communists received 25% of the votes, Nationalists 30%, and Reformists the rest 45%, what will the distribution be in the next election?
What will the distribution be in the third election?
What will the distribution be in the fourth election?
Determine the long term distribution.
a. c.
Given the following absorbing Markov chain.

Find the following:
Identify the absorbing states.
Write the solution matrix.
Starting from state 4, what is the probability of eventual absorption in state 1?
Starting from state 2, what is the probability of eventual absorption in state 3?
1 and 3
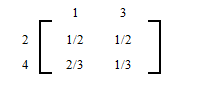
Two tennis players, Andre and Vijay each with two dollars in their pocket, decide to bet each other $1, for every game they play. They continue playing until one of them is broke.
Do the following:
Write the transition matrix for Andre.
Identify the absorbing states.
Write the solution matrix.
At a given stage if Andre has $1, what is the chance that he will eventually lose it all?
Repeat [link] , if the chance of winning for Andre is .4 and for Vijay .6.
Write the transition matrix for Andre.
Write the solution matrix.
If Andre has $3, what is the probability that he will eventually be ruined?
If Vijay has $1, what is the probability that he will eventually triumph?
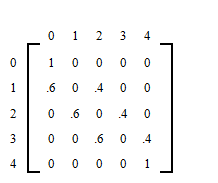
Repeat [link] , if initially Andre has $3 and Vijay has $2.
Write the transition matrix.
Identify the absorbing states.
Write the solution matrix.
If Andre has $4, what is the probability that he will eventually be ruined?
The non-tenured professors at a community college are regularly evaluated. After an evaluation they are classified as good, bad, or improvable. The "improvable" are given a set of recommendations and are re-evaluated the following semester. At the next evaluation, 60% of the improvable turn out to be good, 20% bad, and 20% improvable. These percentages never change and the process continues.
Write the transition matrix.
Identify the absorbing states.
Write the solution matrix.
What is the probability that a professor who is improvable will eventually become good?


Notification Switch
Would you like to follow the 'Applied finite mathematics' conversation and receive update notifications?