6.2 Determining volumes by slicing  (Page 2/12)

Because the cross-sectional area is not constant, we let $A\left(x\right)$ represent the area of the cross-section at point $x.$ Now let $P=\left\{x_0,x_1\text{…},X_n\right\}$ be a regular partition of $\left[a,b\right],$ and for $i=1,2\text{,…}n,$ let $S_i$ represent the slice of $S$ stretching from $x_{i-1}\text{to}{x}_i.$ The following figure shows the sliced solid with $n=3.$

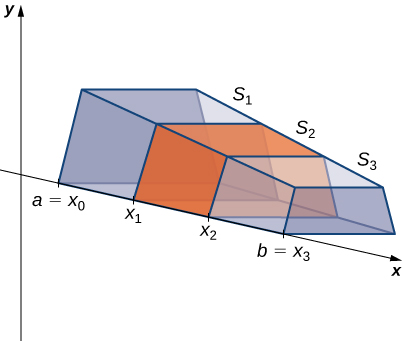
Finally, for $i=1,2\text{,…}n,$ let $x_i^{*}$ be an arbitrary point in $\left[x_{i-1},x_i\right].$ Then the volume of slice $S_i$ can be estimated by $V\left(S_i\right)\approx A\left(x_i^{*}\right)\text{Δ}x.$ Adding these approximations together, we see the volume of the entire solid $S$ can be approximated by

By now, we can recognize this as a Riemann sum, and our next step is to take the limit as $n\to \infty .$ Then we have

The technique we have just described is called the slicing method    . To apply it, we use the following strategy.

Recall that in this section, we assume the slices are perpendicular to the $x\text{-axis}\text{.}$ Therefore, the area formula is in terms of x and the limits of integration lie on the $x\text{-axis}\text{.}$ However, the problem-solving strategy shown here is valid regardless of how we choose to slice the solid.

Deriving the formula for the volume of a pyramid

We know from geometry that the formula for the volume of a pyramid is $V=\frac{1}{3}Ah.$ If the pyramid has a square base, this becomes $V=\frac{1}{3}{a}^{2}h,$ where $a$ denotes the length of one side of the base. We are going to use the slicing method to derive this formula.

We want to apply the slicing method to a pyramid with a square base. To set up the integral, consider the pyramid shown in [link] , oriented along the $x\text{-axis}\text{.}$

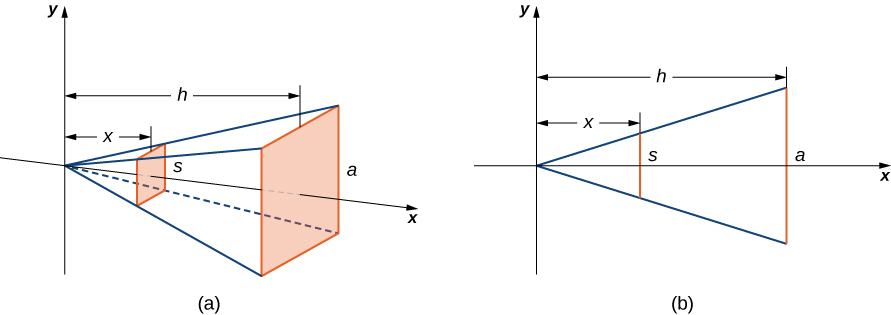
We first want to determine the shape of a cross-section of the pyramid. We are know the base is a square, so the cross-sections are squares as well (step 1). Now we want to determine a formula for the area of one of these cross-sectional squares. Looking at [link] (b), and using a proportion, since these are similar triangles, we have

$\frac{s}{a}=\frac{x}{h}\text{or}s=\frac{ax}{h}.$

Therefore, the area of one of the cross-sectional squares is

$A\left(x\right)=s^2={\left(\frac{ax}{h}\right)}^2\left(\text{step}2\right).$

Then we find the volume of the pyramid by integrating from $0\text{to}h$ (step $3)\text{:}$

$\begin{array}{cc}\hfill V& ={\displaystyle \underset{0}{\overset{h}{\int }}A\left(x\right)}dx\hfill \\ & ={\displaystyle \underset{0}{\overset{h}{\int }}{\left(\frac{ax}{h}\right)}^2}dx=\frac{a^2}{h^2}{\displaystyle \underset{0}{\overset{h}{\int }}{x}^2}dx\hfill \\ & ={\left[\frac{a^2}{h^2}\left(\frac{1}{3}{x}^3\right)\right]|}_0^h=\frac{1}{3}{a}^{2}h.\hfill \end{array}$

This is the formula we were looking for.

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Solids of revolution

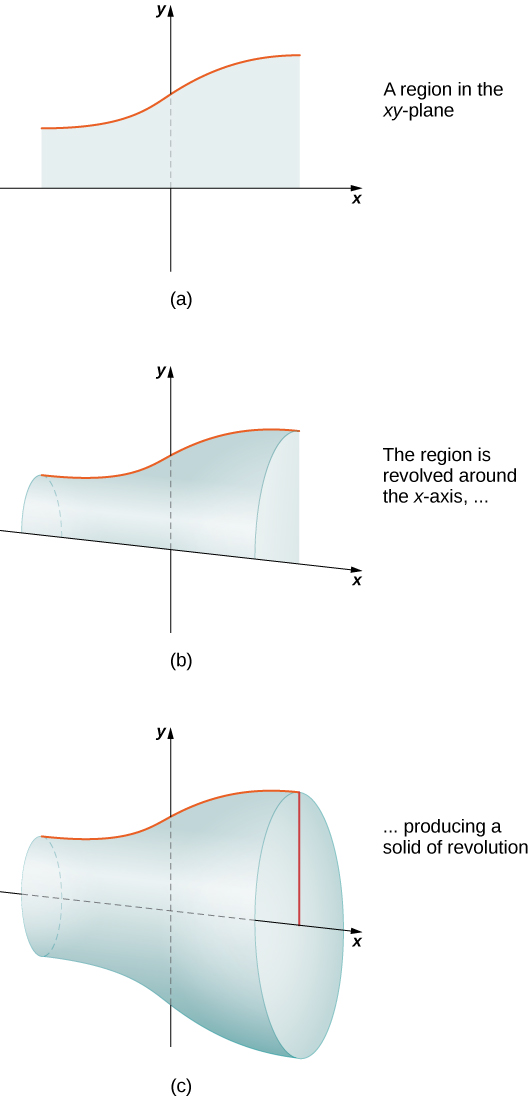
If a region in a plane is revolved around a line in that plane, the resulting solid is called a solid of revolution    , as shown in the following figure.