| << Chapter < Page | Chapter >> Page > |
If and then Differentiating both sides of this equation results in the equation
Solving for yields
Finally, we substitute to obtain
We may also derive this result by applying the inverse function theorem, as follows. Since is the inverse of by applying the inverse function theorem we have
Using this result and applying the chain rule to yields
□
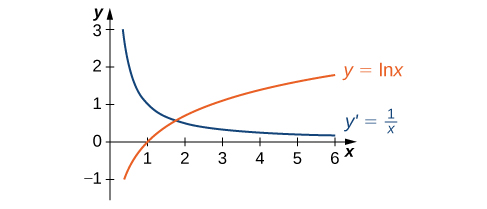
The graph of and its derivative are shown in [link] .
Find the derivative of
Use [link] directly.
Find the derivative of
At first glance, taking this derivative appears rather complicated. However, by using the properties of logarithms prior to finding the derivative, we can make the problem much simpler.
Now that we can differentiate the natural logarithmic function, we can use this result to find the derivatives of and for
Let and let be a differentiable function.
If then It follows that Thus Solving for we have Differentiating and keeping in mind that is a constant, we see that
The derivative in [link] now follows from the chain rule.
If then Using implicit differentiation, again keeping in mind that is constant, it follows that Solving for and substituting we see that
The more general derivative ( [link] ) follows from the chain rule.
□
Find the derivative of
Use the quotient rule and [link] .
Find the slope of the line tangent to the graph of at
To find the slope, we must evaluate at Using [link] , we see that
By evaluating the derivative at we see that the tangent line has slope
At this point, we can take derivatives of functions of the form for certain values of as well as functions of the form where and Unfortunately, we still do not know the derivatives of functions such as or These functions require a technique called logarithmic differentiation , which allows us to differentiate any function of the form It can also be used to convert a very complex differentiation problem into a simpler one, such as finding the derivative of We outline this technique in the following problem-solving strategy.

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?