| << Chapter < Page | Chapter >> Page > |
In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. These applications include acceleration and velocity in physics, population growth rates in biology, and marginal functions in economics.
One application for derivatives is to estimate an unknown value of a function at a point by using a known value of a function at some given point together with its rate of change at the given point. If is a function defined on an interval then the amount of change of over the interval is the change in the values of the function over that interval and is given by
The average rate of change of the function over that same interval is the ratio of the amount of change over that interval to the corresponding change in the values. It is given by
As we already know, the instantaneous rate of change of at is its derivative
For small enough values of We can then solve for to get the amount of change formula:
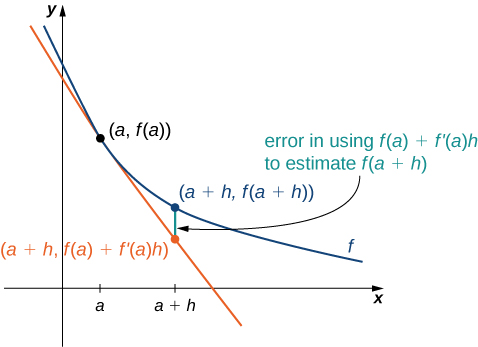
We can use this formula if we know only and and wish to estimate the value of For example, we may use the current population of a city and the rate at which it is growing to estimate its population in the near future. As we can see in [link] , we are approximating by the coordinate at on the line tangent to at Observe that the accuracy of this estimate depends on the value of as well as the value of
Here is an interesting demonstration of rate of change.
If and estimate
Begin by finding We have Thus,
Another use for the derivative is to analyze motion along a line. We have described velocity as the rate of change of position. If we take the derivative of the velocity, we can find the acceleration, or the rate of change of velocity. It is also important to introduce the idea of speed , which is the magnitude of velocity. Thus, we can state the following mathematical definitions.
Let be a function giving the position of an object at time
The velocity of the object at time is given by
The speed of the object at time is given by
The acceleration of the object at is given by

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?