4.8 L’hôpital’s rule  (Page 3/7)

As mentioned, L’Hôpital’s rule is an extremely useful tool for evaluating limits. It is important to remember, however, that to apply L’Hôpital’s rule to a quotient $\frac{f\left(x\right)}{g\left(x\right)},$ it is essential that the limit of $\frac{f\left(x\right)}{g\left(x\right)}$ be of the form $\frac{0}{0}$ or $\infty \text{/}\infty .$ Consider the following example.

Other indeterminate forms

L’Hôpital’s rule is very useful for evaluating limits involving the indeterminate forms $\frac{0}{0}$ and $\infty \text{/}\infty .$ However, we can also use L’Hôpital’s rule to help evaluate limits involving other indeterminate forms that arise when evaluating limits. The expressions $0·\infty ,$ $\infty -\infty ,$ $1^{\infty },$ ${\infty }^0,$ and $0^0$ are all considered indeterminate forms. These expressions are not real numbers. Rather, they represent forms that arise when trying to evaluate certain limits. Next we realize why these are indeterminate forms and then understand how to use L’Hôpital’s rule in these cases. The key idea is that we must rewrite the indeterminate forms in such a way that we arrive at the indeterminate form $\frac{0}{0}$ or $\infty \text{/}\infty .$

Indeterminate form of type $0·\infty$

Suppose we want to evaluate $\underset{x\to a}{\text{lim}}\left(f\left(x\right)·g\left(x\right)\right),$ where $f\left(x\right)\to 0$ and $g\left(x\right)\to \infty$ (or $\text{−}\infty )$ as $x\to a.$ Since one term in the product is approaching zero but the other term is becoming arbitrarily large (in magnitude), anything can happen to the product. We use the notation $0·\infty$ to denote the form that arises in this situation. The expression $0·\infty$ is considered indeterminate because we cannot determine without further analysis the exact behavior of the product $f\left(x\right)g\left(x\right)$ as $x\to \infty .$ For example, let $n$ be a positive integer and consider

As $x\to \infty ,$ $f\left(x\right)\to 0$ and $g\left(x\right)\to \infty .$ However, the limit as $x\to \infty$ of $f\left(x\right)g\left(x\right)=\frac{3x^2}{\left(x^n+1\right)}$ varies, depending on $n.$ If $n=2,$ then $\underset{x\to \infty }{\text{lim}}f\left(x\right)g\left(x\right)=3.$ If $n=1,$ then $\underset{x\to \infty }{\text{lim}}f\left(x\right)g\left(x\right)=\infty .$ If $n=3,$ then $\underset{x\to \infty }{\text{lim}}f\left(x\right)g\left(x\right)=0.$ Here we consider another limit involving the indeterminate form $0·\infty$ and show how to rewrite the function as a quotient to use L’Hôpital’s rule.

Indeterminate form of type $0·\infty$

Evaluate $\underset{x\to 0^{+}}{\text{lim}}x\text{ln}x.$

First, rewrite the function $x\text{ln}x$ as a quotient to apply L’Hôpital’s rule. If we write

$x\text{ln}x=\frac{\text{ln}x}{1\text{/}x},$

we see that $\text{ln}x\to \text{−}\infty$ as $x\to 0^{+}$ and $\frac{1}{x}\to \infty$ as $x\to 0^{+}.$ Therefore, we can apply L’Hôpital’s rule and obtain

$\underset{x\to 0^{+}}{\text{lim}}\frac{\text{ln}x}{1\text{/}x}=\underset{x\to 0^{+}}{\text{lim}}\frac{\frac{d}{dx}\left(\text{ln}x\right)}{\frac{d}{dx}\left(1\text{/}x\right)}=\underset{x\to 0^{+}}{\text{lim}}\frac{1\text{/}{x}^2}{\mathrm{-1}\text{/}x}=\underset{x\to 0^{+}}{\text{lim}}\left(\text{−}x\right)=0.$

We conclude that

$\underset{x\to 0^{+}}{\text{lim}}x\text{ln}x=0.$

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Indeterminate form of type $\infty -\infty$

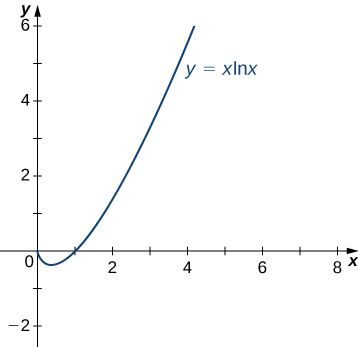
Another type of indeterminate form is $\infty -\infty .$ Consider the following example. Let $n$ be a positive integer and let $f\left(x\right)=3x^n$ and $g\left(x\right)=3x^2+5.$ As $x\to \infty ,$ $f\left(x\right)\to \infty$ and $g\left(x\right)\to \infty .$ We are interested in $\underset{x\to \infty }{\text{lim}}\left(f\left(x\right)-g\left(x\right)\right).$ Depending on whether $f\left(x\right)$ grows faster, $g\left(x\right)$ grows faster, or they grow at the same rate, as we see next, anything can happen in this limit. Since $f\left(x\right)\to \infty$ and $g\left(x\right)\to \infty ,$ we write $\infty -\infty$ to denote the form of this limit. As with our other indeterminate forms, $\infty -\infty$ has no meaning on its own and we must do more analysis to determine the value of the limit. For example, suppose the exponent $n$ in the function $f\left(x\right)=3x^n$ is $n=3,$ then