| << Chapter < Page | Chapter >> Page > |
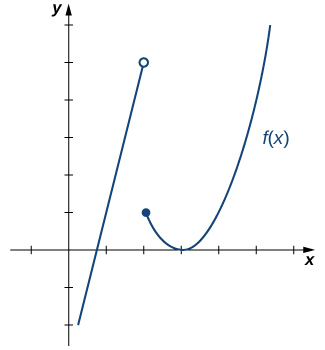
In [link] we look at one-sided limits of a piecewise-defined function and use these limits to draw a conclusion about a two-sided limit of the same function.
For evaluate each of the following limits:
[link] illustrates the function and aids in our understanding of these limits.
We now turn our attention to evaluating a limit of the form where where and That is, has the form at a .
Evaluate
Step 1. After substituting in we see that this limit has the form That is, as x approaches 2 from the left, the numerator approaches −1; and the denominator approaches 0. Consequently, the magnitude of becomes infinite. To get a better idea of what the limit is, we need to factor the denominator:
Step 2. Since is the only part of the denominator that is zero when 2 is substituted, we then separate from the rest of the function:
Step 3. and Therefore, the product of and has a limit of
The techniques we have developed thus far work very well for algebraic functions, but we are still unable to evaluate limits of very basic trigonometric functions. The next theorem, called the squeeze theorem , proves very useful for establishing basic trigonometric limits. This theorem allows us to calculate limits by “squeezing” a function, with a limit at a point a that is unknown, between two functions having a common known limit at a . [link] illustrates this idea.
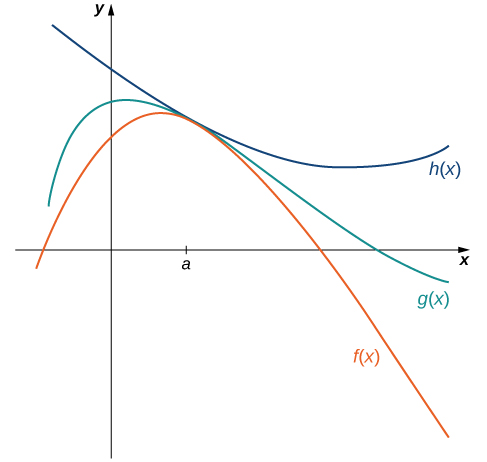
Let and be defined for all over an open interval containing a . If
for all in an open interval containing a and
where L is a real number, then
Apply the squeeze theorem to evaluate
Because for all x , we have for and for (if x is negative the direction of the inequalities changes when we multiply). Since from the squeeze theorem, we obtain The graphs of and are shown in [link] .
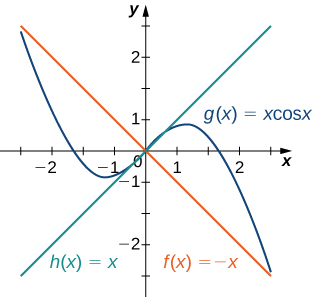
We now use the squeeze theorem to tackle several very important limits. Although this discussion is somewhat lengthy, these limits prove invaluable for the development of the material in both the next section and the next chapter. The first of these limits is Consider the unit circle shown in [link] . In the figure, we see that is the y -coordinate on the unit circle and it corresponds to the line segment shown in blue. The radian measure of angle θ is the length of the arc it subtends on the unit circle. Therefore, we see that for

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?