| << Chapter < Page | Chapter >> Page > |
As we embark on our study of calculus, we shall see how its development arose from common solutions to practical problems in areas such as engineering physics—like the space travel problem posed in the chapter opener. Two key problems led to the initial formulation of calculus: (1) the tangent problem, or how to determine the slope of a line tangent to a curve at a point; and (2) the area problem, or how to determine the area under a curve.
Rate of change is one of the most critical concepts in calculus. We begin our investigation of rates of change by looking at the graphs of the three lines and shown in [link] .
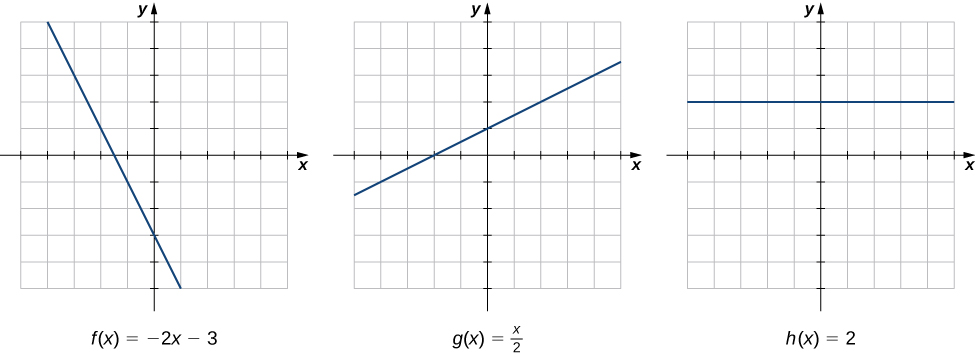
As we move from left to right along the graph of we see that the graph decreases at a constant rate. For every 1 unit we move to the right along the x -axis, the y -coordinate decreases by 2 units. This rate of change is determined by the slope (−2) of the line. Similarly, the slope of 1/2 in the function tells us that for every change in x of 1 unit there is a corresponding change in y of 1/2 unit. The function has a slope of zero, indicating that the values of the function remain constant. We see that the slope of each linear function indicates the rate of change of the function.
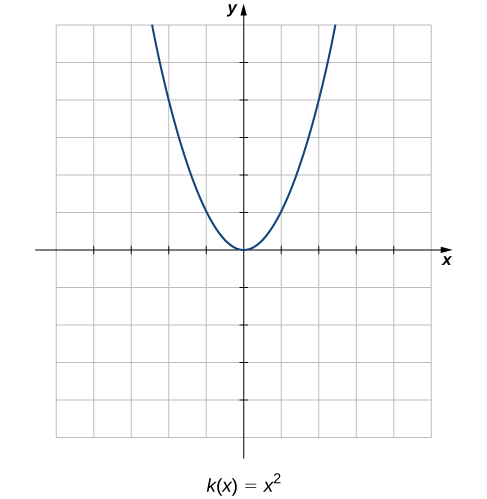
Compare the graphs of these three functions with the graph of ( [link] ). The graph of starts from the left by decreasing rapidly, then begins to decrease more slowly and level off, and then finally begins to increase—slowly at first, followed by an increasing rate of increase as it moves toward the right. Unlike a linear function, no single number represents the rate of change for this function. We quite naturally ask: How do we measure the rate of change of a nonlinear function?
We can approximate the rate of change of a function at a point on its graph by taking another point on the graph of drawing a line through the two points, and calculating the slope of the resulting line. Such a line is called a secant line. [link] shows a secant line to a function at a point
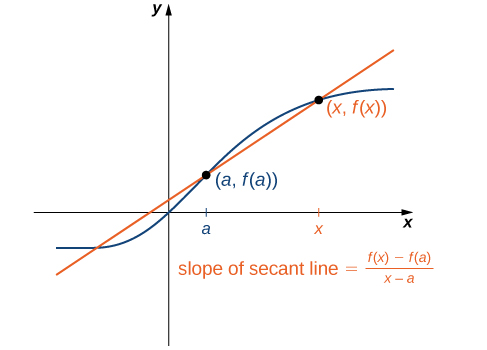
We formally define a secant line as follows:

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?