| << Chapter < Page | Chapter >> Page > |
The steps are summarized below.
To convert scientific notation to decimal form:
Convert to decimal form:
 | |
| Determine the exponent, n , on the factor 10. |
 |
| Since the exponent is negative, move the decimal point 2 places to the left. |
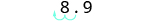 |
| Add zeros as needed for placeholders. |
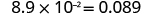 |
Astronomers use very large numbers to describe distances in the universe and ages of stars and planets. Chemists use very small numbers to describe the size of an atom or the charge on an electron. When scientists perform calculations with very large or very small numbers, they use scientific notation. Scientific notation provides a way for the calculations to be done without writing a lot of zeros. We will see how the Properties of Exponents are used to multiply and divide numbers in scientific notation.
Access these online resources for additional instruction and practice with integer exponents and scientific notation:

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?