| << Chapter < Page | Chapter >> Page > |
| Number | Square Root |
|---|---|
| 4 | = 2 |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | = 3 |
The square roots of numbers between 4 and 9 must be between the two consecutive whole numbers 2 and 3, and they are not whole numbers. Based on the pattern in the table above, we could say that must be between 2 and 3. Using inequality symbols, we write:
Estimate between two consecutive whole numbers.
Think of the perfect square numbers closest to 60. Make a small table of these perfect squares and their squares roots.
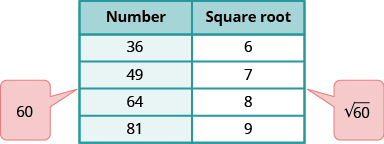 |
|
| Locate 60 between two consecutive perfect squares. |
 |
| is between their square roots. |
 |
Estimate the square root between two consecutive whole numbers.
Estimate the square root between two consecutive whole numbers.
There are mathematical methods to approximate square roots, but nowadays most people use a calculator to find them. Find the key on your calculator. You will use this key to approximate square roots.
When you use your calculator to find the square root of a number that is not a perfect square, the answer that you see is not the exact square root. It is an approximation, accurate to the number of digits shown on your calculator’s display. The symbol for an approximation is and it is read ‘approximately.’
Suppose your calculator has a 10-digit display. You would see that
If we wanted to round to two decimal places, we would say
How do we know these values are approximations and not the exact values? Look at what happens when we square them:
Their squares are close to 5, but are not exactly equal to 5.
Using the square root key on a calculator and then rounding to two decimal places, we can find:
What if we have to find a square root of an expression with a variable? Consider . Can you think of an expression whose square is ?
When we use the radical sign to take the square root of a variable expression, we should specify that to make sure we get the principal square root .
However, in this chapter we will assume that each variable in a square-root expression represents a non-negative number and so we will not write next to every radical.
What about square roots of higher powers of variables? Think about the Power Property of Exponents we used in Chapter 6.
If we square , the exponent will become .
How does this help us take square roots? Let’s look at a few:
Access this online resource for additional instruction and practice with square roots.
Simplify Expressions with Square Roots
In the following exercises, simplify.
Estimate Square Roots
In the following exercises, estimate each square root between two consecutive whole numbers.
Approximate Square Roots
In the following exercises, approximate each square root and round to two decimal places.
Simplify Variable Expressions with Square Roots
In the following exercises, simplify.
Decorating Denise wants to have a square accent of designer tiles in her new shower. She can afford to buy 625 square centimeters of the designer tiles. How long can a side of the accent be?
25 centimeters
Decorating Morris wants to have a square mosaic inlaid in his new patio. His budget allows for 2025 square inch tiles. How long can a side of the mosaic be?
What is the difference between and ?
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?