| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
The definition of a system of linear inequalities is very similar to the definition of a system of linear equations.
Two or more linear inequalities grouped together form a system of linear inequalities .
A system of linear inequalities looks like a system of linear equations, but it has inequalities instead of equations. A system of two linear inequalities is shown below.
To solve a system of linear inequalities, we will find values of the variables that are solutions to both inequalities. We solve the system by using the graphs of each inequality and show the solution as a graph. We will find the region on the plane that contains all ordered pairs that make both inequalities true.
Solutions of a system of linear inequalities are the values of the variables that make all the inequalities true.
The solution of a system of linear inequalities is shown as a shaded region in the x-y coordinate system that includes all the points whose ordered pairs make the inequalities true.
To determine if an ordered pair is a solution to a system of two inequalities, we substitute the values of the variables into each inequality. If the ordered pair makes both inequalities true, it is a solution to the system.
Determine whether the ordered pair is a solution to the system.
ⓐ (−2, 4) ⓑ (3,1)

The ordered pair (−2, 4) made both inequalities true. Therefore (−2, 4) is a solution to this system.
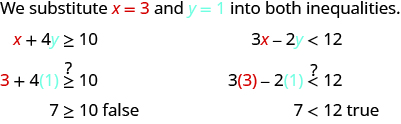
The ordered pair (3,1) made one inequality true, but the other one false. Therefore (3,1) is not a solution to this system.
Determine whether the ordered pair is a solution to the system.
ⓐ ⓑ
ⓐ no ⓑ yes
Determine whether the ordered pair is a solution to the system.
ⓐ ⓑ
ⓐ no ⓑ no
The solution to a single linear inequality is the region on one side of the boundary line that contains all the points that make the inequality true. The solution to a system of two linear inequalities is a region that contains the solutions to both inequalities. To find this region, we will graph each inequality separately and then locate the region where they are both true. The solution is always shown as a graph.

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?