| << Chapter < Page | Chapter >> Page > |
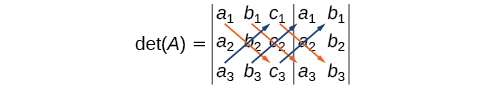
The algebra is as follows:
Find the determinant of the 3 × 3 matrix given
Augment the matrix with the first two columns and then follow the formula. Thus,
Can we use the same method to find the determinant of a larger matrix?
No, this method only works for and matrices. For larger matrices it is best to use a graphing utility or computer software.
Now that we can find the determinant of a 3 × 3 matrix, we can apply Cramer’s Rule to solve a system of three equations in three variables . Cramer’s Rule is straightforward, following a pattern consistent with Cramer’s Rule for 2 × 2 matrices. As the order of the matrix increases to 3 × 3, however, there are many more calculations required.
When we calculate the determinant to be zero, Cramer’s Rule gives no indication as to whether the system has no solution or an infinite number of solutions. To find out, we have to perform elimination on the system.
Consider a 3 × 3 system of equations.
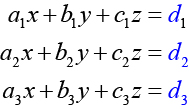
where
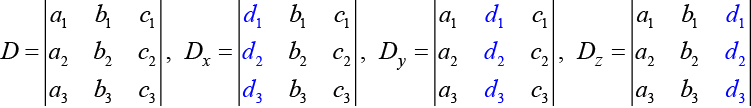
If we are writing the determinant we replace the column with the constant column. If we are writing the determinant we replace the column with the constant column. If we are writing the determinant we replace the column with the constant column. Always check the answer.
Find the solution to the given 3 × 3 system using Cramer’s Rule.
Use Cramer’s Rule.
Then,
The solution is
Solve the system of equations using Cramer’s Rule.
We begin by finding the determinants
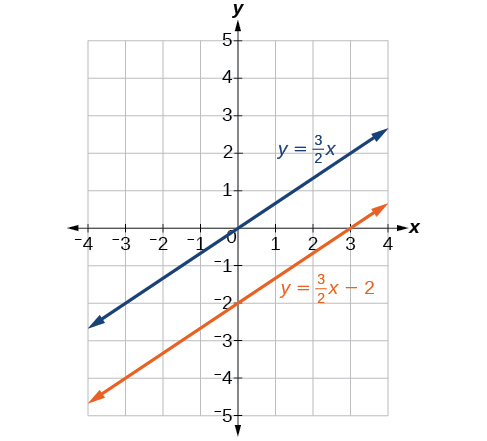
We know that a determinant of zero means that either the system has no solution or it has an infinite number of solutions. To see which one, we use the process of elimination. Our goal is to eliminate one of the variables.
We obtain the equation which is false. Therefore, the system has no solution. Graphing the system reveals two parallel lines. See [link] .
Solve the system with an infinite number of solutions.
Let’s find the determinant first. Set up a matrix augmented by the first two columns.
Then,
As the determinant equals zero, there is either no solution or an infinite number of solutions. We have to perform elimination to find out.
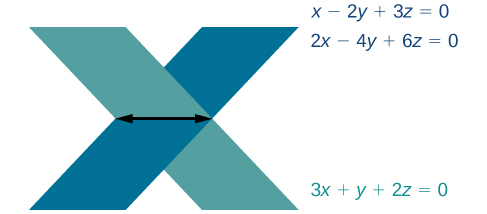

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?