How To
Given a recursive formula with two initial terms, write the first
n terms of a sequence.
Identify the initial term,
a
1
,
which is given as part of the formula.
Identify the second term,
a
2
,
which is given as part of the formula.
To find the third term, substitute the initial term and the second term into the formula. Evaluate.
Repeat until you have evaluated the
n
th term.
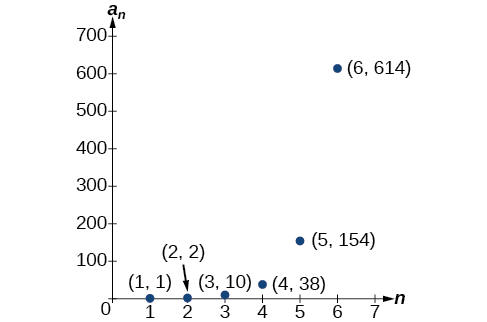
Writing the terms of a sequence defined by a recursive formula
Write the first six terms of the sequence defined by the recursive formula.
a
1
=
1
a
2
=
2
a
n
=
3
a
n
−
1
+
4
a
n
−
2
, for
n
≥
3
The first two terms are given. For each subsequent term, we replace
a
n
−
1 and
a
n
−
2 with the values of the two preceding terms.
n
=
3
a
3
=
3
a
2
+
4
a
1
=
3
(
2
)
+
4
(
1
)
=
10
n
=
4
a
4
=
3
a
3
+
4
a
2
=
3
(
10
)
+
4
(
2
)
=
38
n
=
5
a
5
=
3
a
4
+
4
a
3
=
3
(
38
)
+
4
(
10
)
=
154
n
=
6
a
6
=
3
a
5
+
4
a
4
=
3
(
154
)
+
4
(
38
)
=
614
The first six terms are
{1,2,10,38,154,614}
. See
[link] .
Got questions? Get instant answers now! Got questions? Get instant answers now!
Try It
Write the first 8 terms of the sequence defined by the recursive formula.
a
1
=
0
a
2
=
1
a
3
=
1
a
n
=
a
n
−
1
a
n
−
2
+
a
n
−
3
, for
n
≥
4
{
0
,
1
,
1
,
1
,
2
,
3
,
5
2
,
17
6
}
.
Got questions? Get instant answers now!
Using factorial notation
The formulas for some sequences include products of consecutive positive integers.
n factorial , written as
n
!
, is the product of the positive integers from 1 to
n
. For example,
4
!
=
4
⋅
3
⋅
2
⋅
1
=
24
5
!
=
5
⋅
4
⋅
3
⋅
2
⋅
1
=
120
An example of formula containing a
factorial is
a
n
=
(
n
+
1
)
!
. The sixth term of the sequence can be found by substituting 6 for
n
.
a
6
=
(
6
+
1
)
!
=
7
!
=
7
·
6
·
5
·
4
·
3
·
2
·
1
=
5040
The factorial of any whole number
n is
n
(
n
−
1
)
! We can therefore also think of
5
! as
5
⋅
4
!
.
A General Note
Factorial
n factorial
n
,
denoted
n
!
,
is defined for a positive integer
n as:
0
!
=
1
1
!
=
1
n
!
=
n
(
n
−
1
)
(
n
−
2
)
⋯
(
2
)
(
1
)
, for
n
≥
2
The special case
0
! is defined as
0
!
=
1.
Q&A
Can factorials always be found using a calculator?
No. Factorials get large very quickly—faster than even exponential functions! When the output gets too large for the calculator, it will not be able to calculate the factorial.
Writing the terms of a sequence using factorials
Write the first five terms of the sequence defined by the explicit formula
a
n
=
5
n
(
n
+
2
)
!
.
Substitute
n
=
1
,
n
=
2
,
and so on in the formula.
n
=
1
a
1
=
5
(
1
)
(
1
+
2
)
!
=
5
3
!
=
5
3
·
2
·
1
=
5
6
n
=
2
a
2
=
5
(
2
)
(
2
+
2
)
!
=
10
4
!
=
10
4
·
3
·
2
·
1
=
5
12
n
=
3
a
3
=
5
(
3
)
(
3
+
2
)
!
=
15
5
!
=
15
5
·
4
·
3
·
2
·
1
=
1
8
n
=
4
a
4
=
5
(
4
)
(
4
+
2
)
!
=
20
6
!
=
20
6
·
5
·
4
·
3
·
2
·
1
=
1
36
n
=
5
a
5
=
5
(
5
)
(
5
+
2
)
!
=
25
7
!
=
25
7
·
6
·
5
·
4
·
3
·
2
·
1
=
5
1
,
008
The first five terms are
{
5
6
,
5
12
,
1
8
,
1
36
,
5
1,008
}
.
Got questions? Get instant answers now! Got questions? Get instant answers now!
Key equations
Formula for a factorial
0
!
=
1
1
!
=
1
n
!
=
n
(
n
−
1
)
(
n
−
2
)
⋯
(
2
)
(
1
)
, for
n
≥
2
Key concepts
A sequence is a list of numbers, called terms, written in a specific order.
Explicit formulas define each term of a sequence using the position of the term. See
[link] ,
[link] , and
[link] .
An explicit formula for the
n
th
term of a sequence can be written by analyzing the pattern of several terms. See
[link] .
Recursive formulas define each term of a sequence using previous terms.
Recursive formulas must state the initial term, or terms, of a sequence.
A set of terms can be written by using a recursive formula. See
[link] and
[link] .
A factorial is a mathematical operation that can be defined recursively.
The factorial of
n
is the product of all integers from 1 to
n
See
[link] .