| << Chapter < Page | Chapter >> Page > |
What is an partial sum?
An partial sum is the sum of the first terms of a sequence.
What is the difference between an arithmetic sequence and an arithmetic series?
What is a geometric series?
A geometric series is the sum of the terms in a geometric sequence.
How is finding the sum of an infinite geometric series different from finding the partial sum?
What is an annuity?
An annuity is a series of regular equal payments that earn a constant compounded interest.
For the following exercises, express each description of a sum using summation notation.
The sum of terms from to
The sum of from to
For the following exercises, express each arithmetic sum using summation notation.
For the following exercises, use the formula for the sum of the first terms of each arithmetic sequence.
For the following exercises, express each geometric sum using summation notation.
For the following exercises, use the formula for the sum of the first terms of each geometric sequence, and then state the indicated sum.
For the following exercises, determine whether the infinite series has a sum. If so, write the formula for the sum. If not, state the reason.
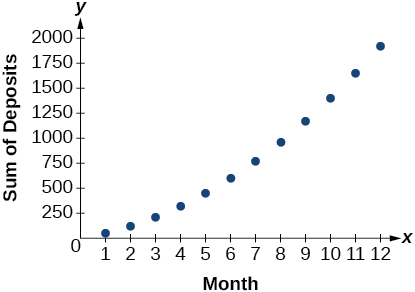
For the following exercises, use the following scenario. Javier makes monthly deposits into a savings account. He opened the account with an initial deposit of $50. Each month thereafter he increased the previous deposit amount by $20.
Graph the arithmetic sequence showing one year of Javier’s deposits.
Graph the arithmetic series showing the monthly sums of one year of Javier’s deposits.
For the following exercises, use the geometric series
Graph the first 7 partial sums of the series.
What number does seem to be approaching in the graph? Find the sum to explain why this makes sense.
Sample answer: The graph of seems to be approaching 1. This makes sense because is a defined infinite geometric series with
For the following exercises, find the indicated sum.
For the following exercises, use the formula for the sum of the first terms of an arithmetic series to find the sum.
For the following exercises, use the formula for the sum of the first terms of a geometric series to find the partial sum.
for the series
For the following exercises, find the sum of the infinite geometric series.
For the following exercises, determine the value of the annuity for the indicated monthly deposit amount, the number of deposits, and the interest rate.
Deposit amount: total deposits: interest rate: compounded monthly
Deposit amount: total deposits: interest rate: compounded monthly
$3,705.42
Deposit amount: total deposits: interest rate: compounded quarterly
Deposit amount: total deposits: interest rate: compounded semi-annually
$695,823.97
The sum of terms from through is What is x ?
Write an explicit formula for such that Assume this is an arithmetic series.
Find the smallest value of n such that
How many terms must be added before the series has a sum less than
9 terms
Write as an infinite geometric series using summation notation. Then use the formula for finding the sum of an infinite geometric series to convert to a fraction.
The sum of an infinite geometric series is five times the value of the first term. What is the common ratio of the series?
To get the best loan rates available, the Riches want to save enough money to place 20% down on a $160,000 home. They plan to make monthly deposits of $125 in an investment account that offers 8.5% annual interest compounded semi-annually. Will the Riches have enough for a 20% down payment after five years of saving? How much money will they have saved?
Karl has two years to save to buy a used car when he graduates. To the nearest dollar, what would his monthly deposits need to be if he invests in an account offering a 4.2% annual interest rate that compounds monthly?
$400 per month
Keisha devised a week-long study plan to prepare for finals. On the first day, she plans to study for hour, and each successive day she will increase her study time by minutes. How many hours will Keisha have studied after one week?
A boulder rolled down a mountain, traveling 6 feet in the first second. Each successive second, its distance increased by 8 feet. How far did the boulder travel after 10 seconds?
420 feet
A scientist places 50 cells in a petri dish. Every hour, the population increases by 1.5%. What will the cell count be after 1 day?
A pendulum travels a distance of 3 feet on its first swing. On each successive swing, it travels the distance of the previous swing. What is the total distance traveled by the pendulum when it stops swinging?
12 feet
Rachael deposits $1,500 into a retirement fund each year. The fund earns 8.2% annual interest, compounded monthly. If she opened her account when she was 19 years old, how much will she have by the time she is 55? How much of that amount will be interest earned?

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?